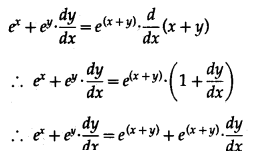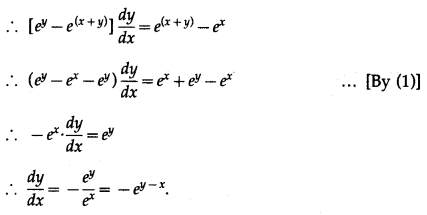12th Commerce Maths 1 Chapter 3 Exercise 3.4 Answers Maharashtra Board

Differentiation Class 12 Commerce Maths 1 Chapter 3 Exercise 3.4 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 3 Differentiation Ex 3.4 Questions and Answers.

Std 12 Maths 1 Exercise 3.4 Solutions Commerce Maths

1. Find \(\frac{d y}{d x}\) if:

Question 1.
√x + √y = √a
Solution:
√x + √y = √a
Differentiating both sides w.r.t. x, we get

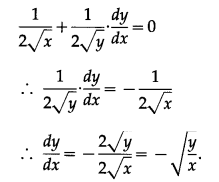
Question 2.
x ³ + y ³ + 4x ³ y = 0
Solution:
x ³ + y ³ + 4x ³ y = 0
Differentiating both sides w.r.t. x, we get

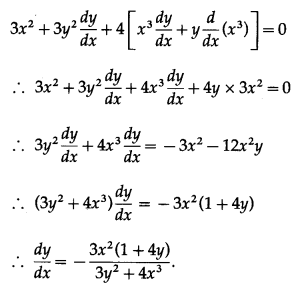
Question 3.
x ³ + x ² y + xy ² + y ³ = 81
Solution:
x ³ + x ² y + xy ² + y ³ = 81
Differentiating both sides w.r.t. x, we get

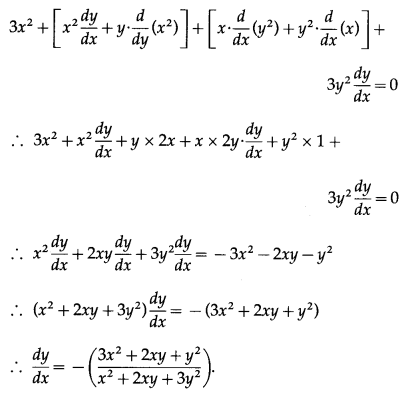
2. Find \(\frac{d y}{d x}\) if:

Question 1.
y.e ^x + x.e ^y = 1
Solution:
y.e ^x + x.e ^y = 1
Differentiating both sides w.r.t. x, we get

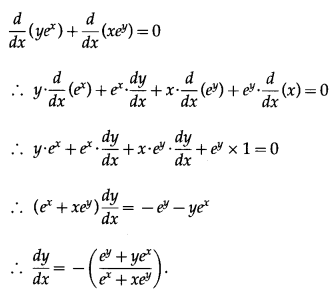
Question 2.
x ^y = e ^(x-y)
Solution:
x ^y = e ^(x-y)
∴ log x ^y = log e ^(x-y)
∴ y log x = (x – y) log e
∴ y log x = x – y …..[∵ log e = 1]
∴ y + y log x = x
∴ y(1 + log x) = x
∴ y = \(\frac{x}{1+\log x}\)

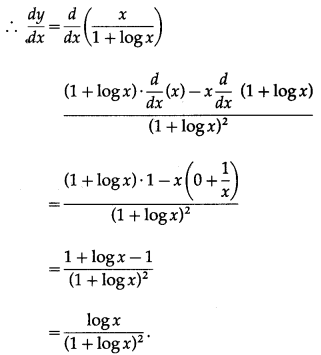
Question 3.
xy = log(xy)
Solution:
xy = log (xy)
∴ xy = log x + log y
Differentiating both sides w.r.t. x, we get

3. Solve the following:

Question 1.
If x ⁵ . y ⁷ = (x + y) ¹² , then show that \(\frac{d y}{d x}=\frac{y}{x}\)
Solution:
x ⁵ . y ⁷ = (x + y) ¹²
∴ log(x ⁵ . y ⁷ ) = log(x + y) ¹²
∴ log x ⁵ + log y ⁷ = log(x + y) ¹²
∴ 5 log x + 7 log y = 12 log (x + y)
Differentiating both sides w.r.t. x, we get

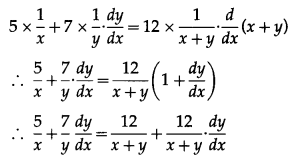
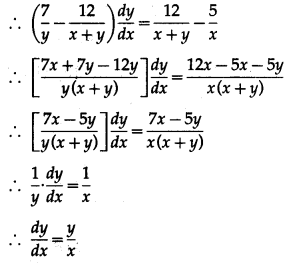
Question 2.
If log(x + y) = log(xy) + a, then show that \(\frac{d y}{d x}=\frac{-y^{2}}{x^{2}}\)
Solution:
log (x + y) = log (xy) + a
∴ log(x + y) = log x + log y + a
Differentiating both sides w.r.t. x, we get

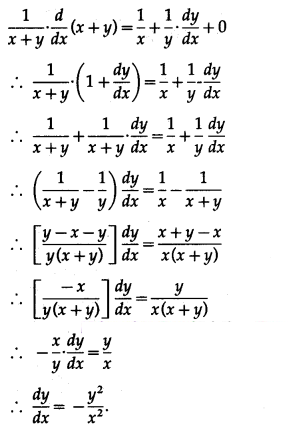
Question 3.
If e ^x + e ^y = e ^(x+y) , then show that \(\frac{d y}{d x}=-e^{y-x}\).
Solution:
e ^x + e ^y = e ^(x+y) ……….(1)
Differentiating both sides w.r.t. x, we get