12th Commerce Maths 1 Chapter 4 Miscellaneous Exercise 4 Answers Maharashtra Board

Applications of Derivatives Class 12 Commerce Maths 1 Chapter 4 Miscellaneous Exercise 4 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 4 Applications of Derivatives Miscellaneous Exercise 4 Questions and Answers.

Std 12 Maths 1 Miscellaneous Exercise 4 Solutions Commerce Maths

(I) Choose the correct alternative:

Question 1.
The equation of tangent to the curve y = x ² + 4x + 1 at (-1, -2) is
(a) 2x – y = 0
(b) 2x + y – 5 = 0
(c) 2x – y – 1 = 0
(d) x + y – 1 = 0
Answer:
(a) 2x – y = 0

Question 2.
The equation of tangent to the curve x ² + y ² = 5, where the tangent is parallel to the line 2x – y + 1 = 0 are
(a) 2x – y + 5 = 0; 2x – y – 5 = 0
(b) 2x + y + 5 = 0; 2x + y – 5 = 0
(c) x – 2y + 5 = 0; x – 2y – 5 = 0
(d) x + 2y + 5; x + 2y – 5 = 0
Answer:
(a) 2x – y + 5 = 0; 2x – y – 5 = 0

Question 3.
If the elasticity of demand η = 1, then demand is
(a) constant
(b) inelastic
(c) unitary elastic
(d) elastic
Answer:
(c) unitary elastic

Question 4.
If 0 < η < 1, then the demand is
(a) constant
(b) inelastic
(c) unitary elastic
(d) elastic
Answer:
(b) inelastic

Question 5.
The function f(x) = x ³ – 3x ² + 3x – 100, x ∈ R is
(a) increasing for all x ∈ R, x ≠ 1
(b) decreasing
(c) neither increasing nor decreasing
(d) decreasing for all x ∈ R, x ≠ 1
Answer:
(a) increasing for all x ∈ R, x ≠ 1

Question 6.
If f(x) = 3x ³ – 9x ² – 27x + 15, then
(a) f has maximum value 66
(b) f has minimum value 30
(c) f has maxima at x = -1
(d) f has minima at x = -1
Answer:
(c) f has maxima at x = -1

(II) Fill in the blanks:

Question 1.
The slope of tangent at any point (a, b) is called as ___________
Answer:
gradient

Question 2.
If f(x) = x ³ – 3x ² + 3x – 100, x ∈ R, then f”(x) is ___________
Answer:
6x – 6 = 6(x – 1)

Question 3.
If f(x) = \(\frac{7}{x}\) – 3, x ∈ R, x ≠ 0, then f”(x) is ___________
Answer:
14x ^-3

Question 4.
A rod of 108 m in length is bent to form a rectangle. If area j at the rectangle is maximum, then its dimensions are ___________
Answer:
27 and 27

Question 5.
If f(x) = x . log x, then its maximum value is ___________
Answer:
\(-\frac{1}{e}\)

(III) State whether each of the following is True or False:

Question 1.
The equation of tangent to the curve y = 4xe ^x at (-1, \(\frac{-4}{e}\)) is y.e + 4 = 0.
Answer:
True

Question 2.
x + 10y + 21 = 0 is the equation of normal to the curve y = 3x ² + 4x – 5 at (1, 2).
Answer:
False

Question 3.
An absolute maximum must occur at a critical point or at an endpoint.
Answer:
True

Question 4.
The function f(x) = x.e ^x(1-x) is increasing on (\(\frac{-1}{2}\), 1).
Answer:
True.
Hint:


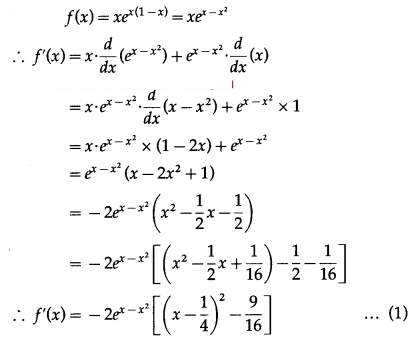
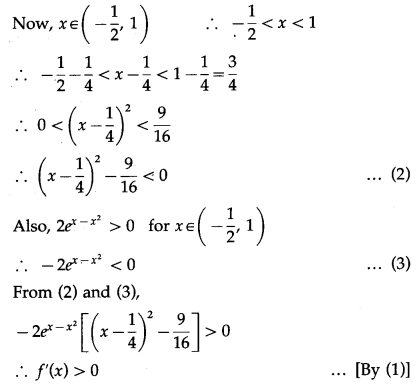
Hence, function f(x) is increasing on (\(\frac{-1}{2}\), 1).

(IV) Solve the following:

Question 1.
Find the equations of tangent and normal to the following curves:
(i) xy = c ² at (ct, \(\frac{c}{t}\)), where t is a parameter.
Solution:
xy = c ²
Differentiating both sides w.r.t. x, we get


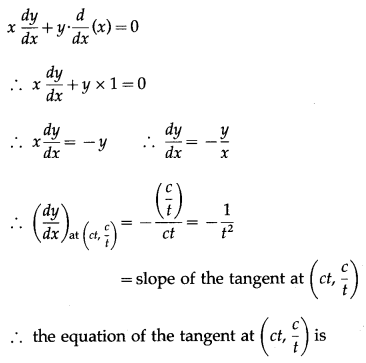
Hence, equations of tangent and normal are x + t ² y – 2ct = 0 and t ³ x – ty – c(t ⁴ + 1) = 0 respectively.

(ii) y = x ² + 4x at the point whose ordinate is -3.
Solution:
Let P(x ₁ , y ₁ ) be the point on the curve
y = x ² + 4x, where y ₁ = -3



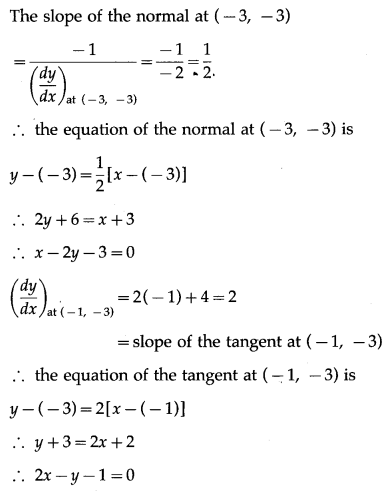
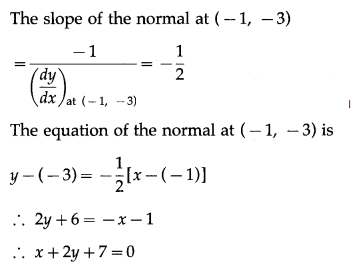
Hence, the equations of tangent and normal at
(i) (-3, -3) are 2x + y + 9 = 0 and x – 2y – 3 = 0
(ii) (-1, -3) are 2x – y – 1 = 0 and x + 2y + 7 = 0

(iii) x = \(\frac{1}{t}\), y = t – \(\frac{1}{t}\), at t = 2.
Solution:
When t = 2, x = \(\frac{1}{2}\) and y = 2 – \(\frac{1}{2}\) = \(\frac{3}{2}\)
Hence, the point P at which we want to find the equations of tangent and normal is (\(\frac{1}{2}\), \(\frac{3}{2}\))



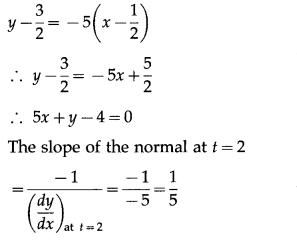
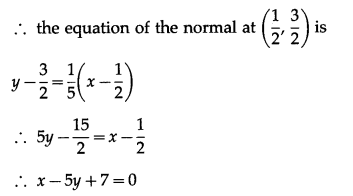
Hence, the equations of tangent and normal are 5x + y – 4 = 0 and x – 5y + 7 = 0 respectively.

(iv) y = x ³ – x ² – 1 at the point whose abscissa is -2.
Solution:
y = x ³ – x ² – 1
∴ \(\frac{d y}{d x}=\frac{d}{d x}\)(x ³ – x ² – 1)
= 3x ² – 2x – 0
= 3x ² – 2x
∴ \(\left(\frac{d y}{d x}\right)_{\text {at } x=-2}\) = 3(-2) ² – 2(-2) = 16
= slope of the tangent at x = -2
When x = -2, y = (-2) ³ – (-2) ² – 1 = -13
∴ the point P is (-2, -13)
∴ the equation of the tangent at (-2, -13) is
y – (-13) = 16[x – (-2)]
∴ y + 13 = 16x + 32
∴ 16x – y + 19 = 0
The slope of the normal at x = -2
= \(\frac{-1}{\left(\frac{d y}{d x}\right)_{\text {at } x=-2}}=\frac{-1}{16}\)
∴ the equation of the normal at (-2, -13) is
y – (-13) = \(-\frac{1}{16}\)[x – (-2)]
∴ 16y + 208 = -x – 2
∴ x + 16y + 210 = 0
Hence, equations of tangent and normal are 16x – y + 19 = 0 and x + 16y + 210 = 0 respectively.

Question 2.
Find the equation of the normal to the curve y = \(\sqrt{x-3}\) which is perpendicular to the line 6x + 3y – 4 = 0.
Solution:
Let P(x ₁ , y ₁ ) be the foot of the required normal to the curve y = \(\sqrt{x-3}\)
Differentiating y = \(\sqrt{x-3}\) w.r.t. x, we get



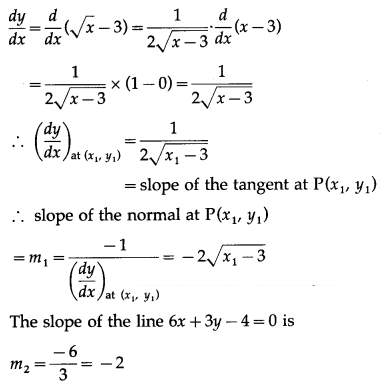
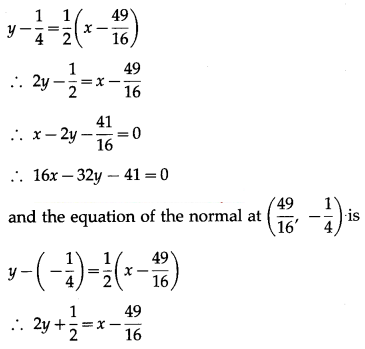
∴ x – 2y – \(\frac{57}{16}\) = 0
i.e. 16x – 32y – 57 = 0
Hence, the equation of the normals are 16x – 32y – 41 = 0 and 16x – 32y – 57 = 0.

Question 3.
Show that the function f(x) = \(\frac{x-2}{x+1}\), x ≠ -1 is increasing.
Solution:
f(x) = \(\frac{x-2}{x+1}\)

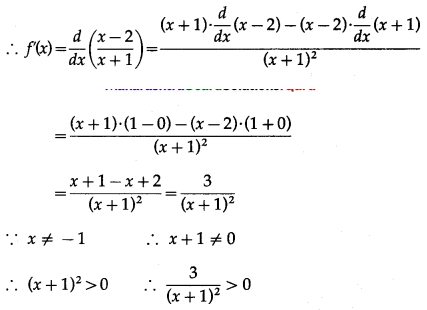
∴ f'(x) > 0, for all x ∈ R, x ≠ -1
Hence, the function f is increasing for all x ∈ R, where x ≠ -1.

Question 4.
Show that the function f(x) = \(\frac{3}{x}\) + 10, x ≠ 0 is decreasing.
Solution:
f(x) = \(\frac{3}{x}\) + 10

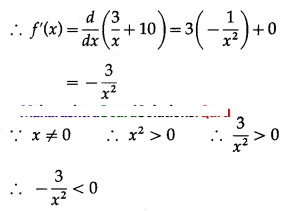
∴ f'(x) < 0 for all x ∈ R, x ≠ 0
Hence, the function f is decreasing for all x ∈ R, where x ≠ 0.

Question 5.
If x + y = 3, show that the maximum value of x ² y is 4.
Solution:
x + y = 3
∴ y = 3 – x
∴ x ² y = x ² (3 – x) = 3x ² – x ³
Let f(x) = 3x ² – x ³
Then f'(x) = \(\frac{d}{d x}\)(3x ² – x ³ )
= 3 × 2x – 3x ²
= 6x – 3x ²
and f”(x) = \(\frac{d}{d x}\)(6x – 3x ² )
= 6 × 1 – 3 × 2x
= 6 – 6x
Now, f'(x) = 0 gives 6x – 3x ² = 0
∴ 3x(2 – x) = 0
∴ x = 0 or x = 2
f”(0) = 6 – 0 = 6 > 0
∴ f has minimum value at x = 0
Also, f”(2) = 6 – 12 = -6 < 0
∴ f has maximum value at x = 2
When x = 2, y = 3 – 2 = 1
∴ maximum value of x ² y = (2) ² (1) = 4.

Question 6.
Examine the function f for maxima and minima, where f(x) = x ³ – 9x ² + 24x.
Solution:
f(x) = x ³ – 9x ² + 24x
∴ f'(x) = \(\frac{d}{d x}\)(x ³ – 9x ² + 24x)
= 3x ² – 9 × 2x + 24 × 1
= 3x ² – 18x + 24
and f”(x) = \(\frac{d}{d x}\)(3x ² – 18x + 24)
= 3 × 2x – 18 × 1 + 0
= 6x – 18
f'(x) = 0 gives 3x ² – 18x + 24 = 0
∴ x ² – 6x + 8 = 0
∴ (x – 2)(x – 4) = 0
∴ the roots of f'(x) = 0 are x ₁ = 2 and x ₂ = 4.
(a) f”(2) = 6(2) – 18 = -6 < 0
∴ by the second derivative test,
f has maximum at x = 2 and maximum value of f at x = 2
f(2) = (2) – 9(2) ² + 24(2)
= 8 – 36 + 48
= 20
(b) f”(4) = 6(4) – 18 = 6 > 0
∴ by the second derivative test, f has minimum at x = 4
and minimum value of f at x = 4
f(4) = (4) ³ – 9(4) ² + 24(4)
= 64 – 144 + 96
= 16.