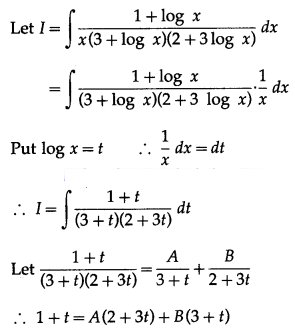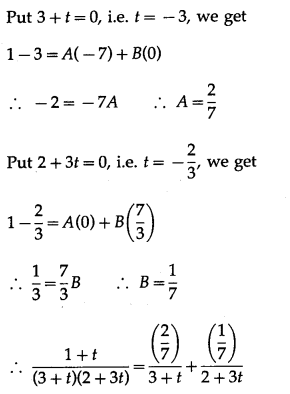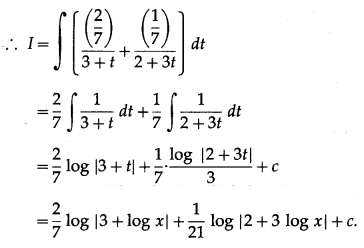12th Commerce Maths 1 Chapter 5 Miscellaneous Exercise 5 Answers Maharashtra Board

Integration Class 12 Commerce Maths 1 Chapter 5 Miscellaneous Exercise 5 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Miscellaneous Exercise 5 Questions and Answers.

Std 12 Maths 1 Miscellaneous Exercise 5 Solutions Commerce Maths

(I) Choose the correct alternative from the following:

Question 1.
The value of \(\int \frac{d x}{\sqrt{1-x}}\) is
(a) 20\(\sqrt{1-x}\) + c
(b) -2\(\sqrt{1-x}\) + c
(c) √x + c
(d) x + c
Answer:
(b) -2\(\sqrt{1-x}\) + c

Question 2.
\(\int \sqrt{1+x^{2}} d x\) =
(a) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left(x+\sqrt{1+x^{2}}\right)+c\)
(b) \(\frac{2}{3}\left(1+x^{2}\right)^{3 / 2}+c\)
(c) \(\frac{1}{3}\left(1+x^{2}\right)+c\)
(d) \(\frac{(x)}{\sqrt{1+x^{2}}}+c\)
Answer:
(a) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left(x+\sqrt{1+x^{2}}\right)+c\)

Question 3.
\(\int x^{2}(3)^{x^{3}} d x\) =
(a) \(\text { (3) }^{x^{3}}+c\)
(b) \(\frac{(3)^{x^{3}}}{3 \cdot \log 3}+c\)
(c) \(\log 3(3)^{x^{3}}+c\)
(d) \(x^{2}(3)^{x 3}\)
Answer:
(b) \(\frac{(3)^{x^{3}}}{3 \cdot \log 3}+c\)
Hint:
Put x ³ = t

Question 4.
\(\int \frac{x+2}{2 x^{2}+6 x+5} d x=p \int \frac{4 x+6}{2 x^{2}+6 x+5} d x\) + \(\frac{1}{2} \int \frac{d x}{2 x^{2}+6 x+5}\), then p = __________
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{4}\)
(d) 2
Answer:
(c) \(\frac{1}{4}\)
Hint:
\(\int \frac{x+2}{2 x^{2}+6 x+5} d x=\int \frac{\frac{1}{4}(4 x+6)+\frac{1}{2}}{2 x^{2}+6 x+5} d x\)

Question 5.
\(\int \frac{d x}{\left(x-x^{2}\right)}\) = ________
(a) log x – log(1 – x) + c
(b) log(1 – x ² ) + c
(c) -log x + log(1 – x) + c
(d) log(x – x ² ) + c
Answer:
(a) log x – log(1 – x) + c

Question 6.
\(\int \frac{d x}{(x-8)(x+7)}\) = __________
(a) \(\frac{1}{15} \log \left|\frac{x+2}{x-1}\right|+c\)
(b) \(\frac{1}{15} \log \left|\frac{x+8}{x+7}\right|+c\)
(c) \(\frac{1}{15} \log \left|\frac{x-8}{x+7}\right|+c\)
(d) (x – 8)(x – 7) + c
Answer:
(c) \(\frac{1}{15} \log \left|\frac{x-8}{x+7}\right|+c\)

Question 7.
\(\int\left(x+\frac{1}{x}\right)^{3} d x\) = _________
(a) \(\frac{1}{4}\left(x+\frac{1}{x}\right)^{4}+c\)
(b) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x-\frac{1}{2 x^{2}}+c\)
(c) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x+\frac{1}{x^{2}}+c\)
(d) \(\left(x-x^{-1}\right)^{3}+c\)
Answer:
(b) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x-\frac{1}{2 x^{2}}+c\)
Hint:
\(\left(x+\frac{1}{x}\right)^{3}=x^{3}+3 x+\frac{3}{x}+\frac{1}{x^{3}}\)

Question 8.
\(\int\left(\frac{e^{2 x}+e^{-2 x}}{e^{x}}\right) d x\)
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)
(b) \(e^{x}+\frac{1}{3 e^{3 x}}+c\)
(c) \(e^{-x}+\frac{1}{3 e^{3 x}}+c\)
(d) \(e^{-x}-\frac{1}{3 e^{3 x}}+c\)
Answer:
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)

Question 9.
∫(1 – x) ^-2 dx = ___________
(a) (1 + x) ^-1 + c
(b) (1 – x) ^-1 + c
(c) (1 – x) ^-1 – 1 + c
(d) (1 – x) ^-1 + 1 + c
Answer:
(b) (1 – x) ^-1 + c

Question 10.
\(\int \frac{\left(x^{3}+3 x^{2}+3 x+1\right)}{(x+1)^{5}} d x\) = _______
(a) \(\frac{-1}{x+1}+c\)
(b) \(\left(\frac{-1}{x+1}\right)^{5}+c\)
(c) log(x + 1) + c
(d) log|x + 1| ⁵ + c
Answer:
(a) \(\frac{-1}{x+1}+c\)
Hint:
x ³ + 3x ² + 3x + 1 = (x + 1) ³

(II) Fill in the blanks.

Question 1.
\(\int \frac{5\left(x^{6}+1\right)}{x^{2}+1}\)dx = x ⁴ + ___x ³ + 5x + c.
Answer:
\(-\frac{5}{3}\)
Hint:
x ⁶ + 1 = (x ² + 1)(x ⁴ – x ² + 1)

Question 2.
\(\int \frac{x^{2}+x-6}{(x-2)(x-1)} d x\) = x + ______ + c
Answer:
4 log|x – 1|
Hint:
x ² + x – 6 = (x + 3)(x – 2)

Question 3.
If f'(x) = \(\frac{1}{x}\) + x and f(1) = \(\frac{5}{2}\) then f(x) = log x + \(\frac{x^{2}}{2}\) + _______
Answer:
2
Hint:

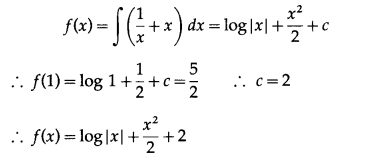
Question 4.
To find the value of \(\int \frac{(1+\log x) d x}{x}\) the proper substitution is __________
Answer:
1 + log x = t

Question 5.
\(\int \frac{1}{x^{3}}\left[\log x^{x}\right]^{2} d x\) = p(log x) ³ + c, then p = _______
Answer:
\(\frac{1}{3}\)
Hint:
\(\frac{1}{x^{3}}\left(\log x^{x}\right)^{2}=\frac{1}{x^{3}}(x \log x)^{2}=\frac{(\log x)^{2}}{x}\)

(III) State whether each of the following is True or False:

Question 1.
The proper substitution for \(\int x\left(x^{x}\right)^{x}(2 \log x+1) d x \text { is }\left(x^{x}\right)^{x}=t\)
Answer:
True

Question 2.
If ∫x e ^2x dx is equal to e ^2x f(x) + c where c is constant of integration, then f(x) is \(\frac{(2 x-1)}{2}\).
Answer:
False

Question 3.
If ∫x f(x) dx = \(\frac{f(x)}{2}\), then f(x) = \(e^{x^{2}}\).
Answer:
True

Question 4.
If \(\int \frac{(x-1) d x}{(x+1)(x-2)}\) = A log|x + 1| + B log|x – 2|, then A + B = 1.
Answer:
True

Question 5.
For \(\int \frac{x-1}{(x+1)^{3}} e^{x} d x\) = e ^x f(x) + c, f(x) = (x + 1) ² .
Answer:
False

(IV) Solve the following:

1. Evaluate:

(i) \(\int \frac{5 x^{2}-6 x+3}{2 x-3} d x\)
Solution:

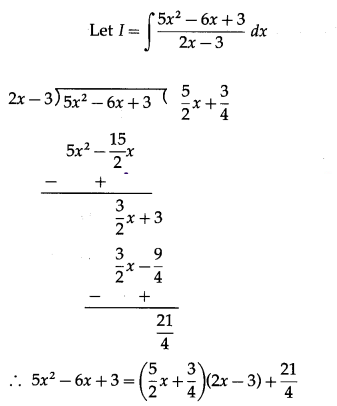
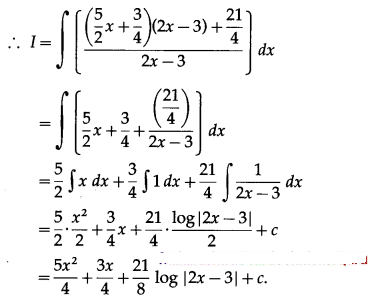
(ii) \(\int(5 x+1)^{\frac{4}{9}} d x\)
Solution:

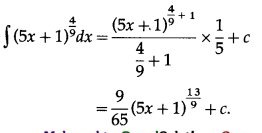
(iii) \(\int \frac{1}{2 x+3} d x\)
Solution:

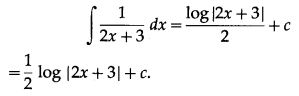
(iv) \(\int \frac{x-1}{\sqrt{x+4}} d x\)
Solution:

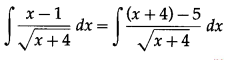
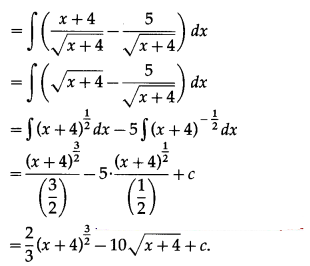
(v) If f'(x) = √x and f(1) = 2, then find the value of f(x).
Solution:
By the definition of integral

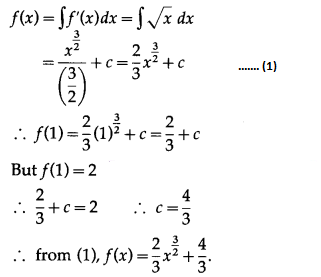
(vi) ∫|x| dx if x < 0
Solution:
∫|x| dx = ∫-x dx …..[∵ x < 0]
= -∫x dx
= \(-\frac{x^{2}}{2}\) + c

2. Evaluate:

(i) Find the primitive of \(\frac{1}{1+e^{x}}\)
Solution:
Let I be the primitive of \(\frac{1}{1+e^{x}}\)

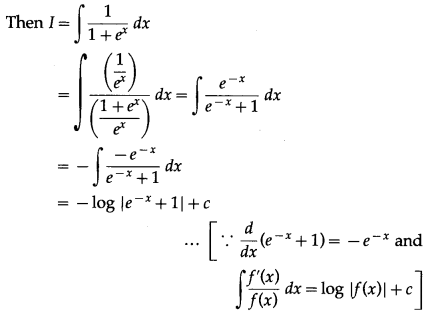
(ii) \(\int \frac{a e^{x}+b e^{-x}}{\left(a e^{x}-b e^{-x}\right)^{2}} d x\)
Solution:

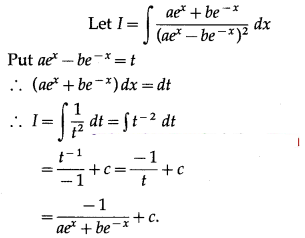
(iii) \(\int \frac{1}{2 x+3 x \log x} d x\)
Solution:

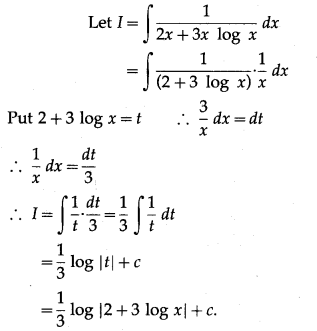
(iv) \(\int \frac{1}{\sqrt{x}+x} d x\)
Solution:

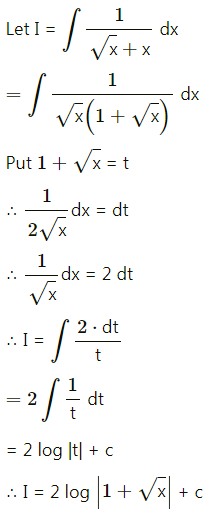
(v) \(\int \frac{2 e^{x}-3}{4 e^{x}+1} d x\)
Solution:

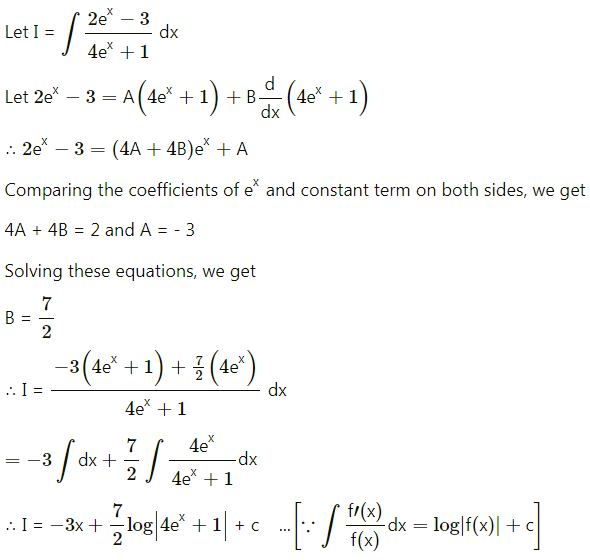
3. Evaluate:

(i) \(\int \frac{d x}{\sqrt{4 x^{2}-5}} d x\)
Solution:

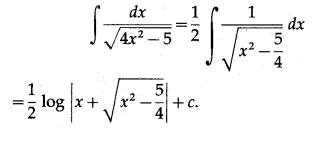
(ii) \(\int \frac{d x}{3-2 x-x^{2}} d x\)
Solution:

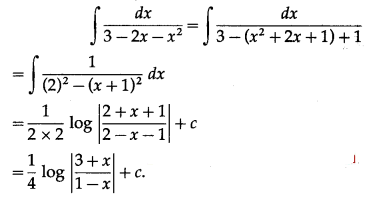
(iii) \(\int \frac{d x}{9 x^{2}-25}\)
Solution:

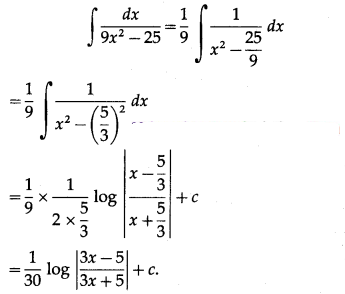
(iv) \(\int \frac{e^{x}}{\sqrt{e^{2 x}+4 e^{x}+13}} d x\)
Solution:

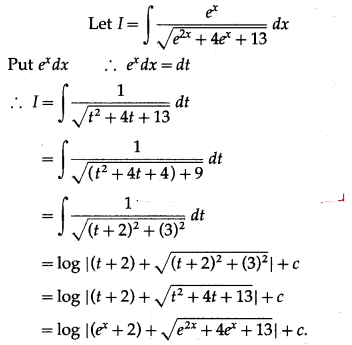
(v) \(\int \frac{d x}{x\left[(\log x)^{2}+4 \log x-1\right]}\)
Solution:

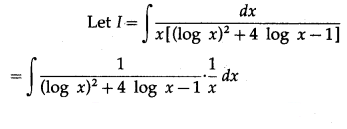
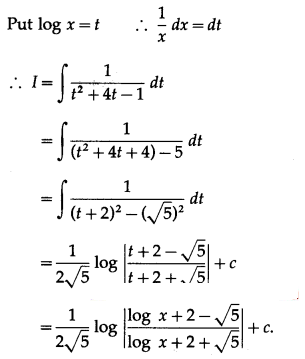
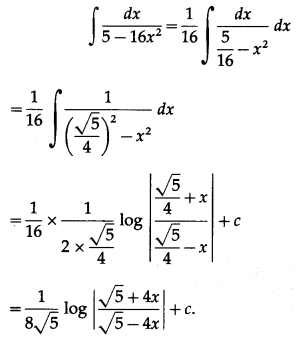
(vi) \(\int \frac{d x}{5-16 x^{2}}\)
Solution:

(vii) \(\int \frac{d x}{25 x-x(\log x)^{2}}\)
Solution:

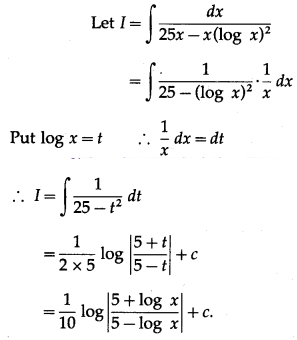
(viii) \(\int \frac{e^{x}}{4 e^{2 x}-1} d x\)
Solution:

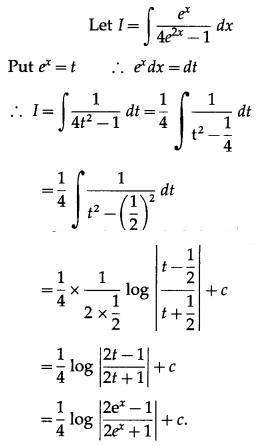
4. Evaluate:

(i) ∫(log x) ² dx
Solution:

(ii) \(\int e^{x} \frac{1+x}{(2+x)^{2}} d x\)
Solution:

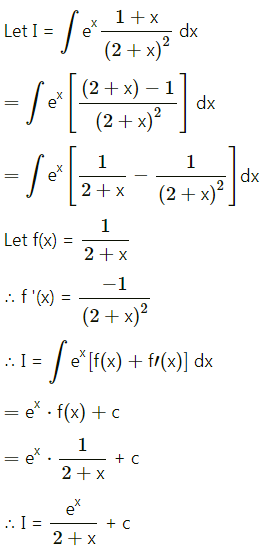
(iii) ∫x e ^2x dx
Solution:

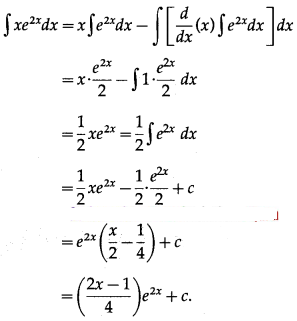
(iv) ∫log(x ² + x) dx
Solution:

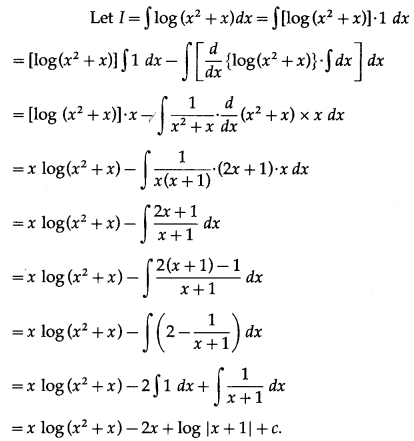
(v) \(\int e^{\sqrt{x}} d x\)
Solution:

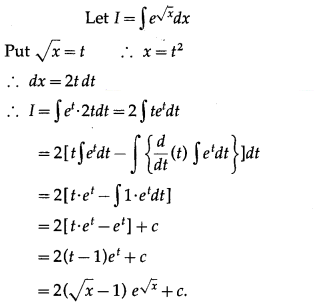
(vi) \(\int \sqrt{x^{2}+2 x+5} d x\)
Solution:

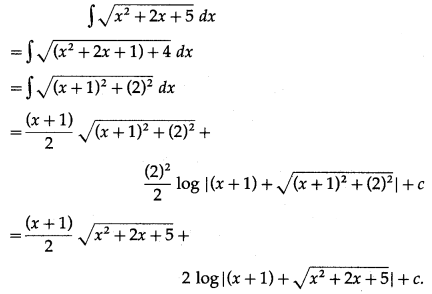
(vii) \(\int \sqrt{x^{2}-8 x+7} d x\)
Solution:

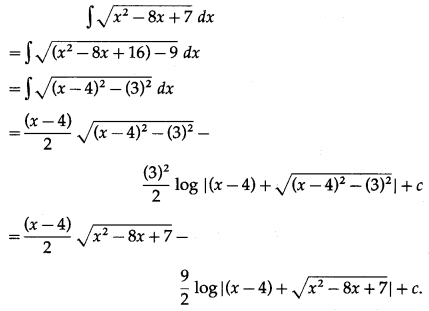
5. Evaluate:

(i) \(\int \frac{3 x-1}{2 x^{2}-x-1} d x\)
Solution:

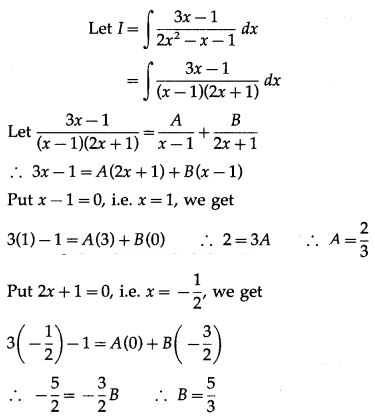
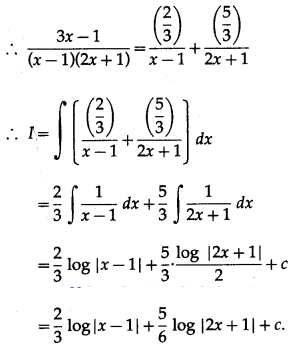
(ii) \(\int \frac{2 x^{3}-3 x^{2}-9 x+1}{2 x^{2}-x-10} d x\)
Solution:

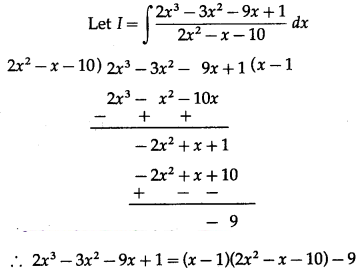
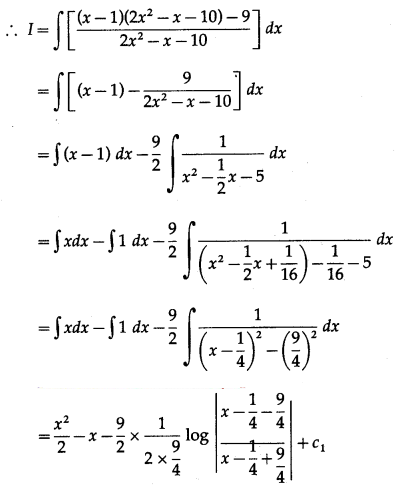
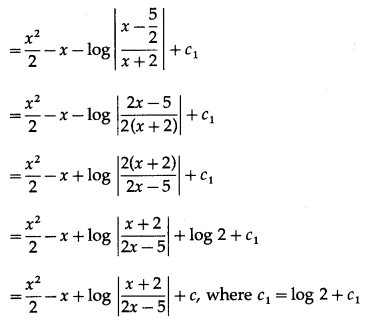
(iii) \(\int \frac{1+\log x}{x(3+\log x)(2+3 \log x)} d x\)
Solution: