Linear Programming Class 12 Commerce Maths 2 Chapter 6 Exercise 6.2 Answers Maharashtra Board
Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 6 Linear Programming Ex 6.2 Questions and Answers.
Std 12 Maths 2 Exercise 6.2 Solutions Commerce Maths
Solve the following LPP by graphical method.
Question 1.
Maximize z = 11x + 8y, Subject to x ≤ 4 ,y ≤ 6 x + y ≤ 6, x ≥ 0, y ≥ 0.
Solution:
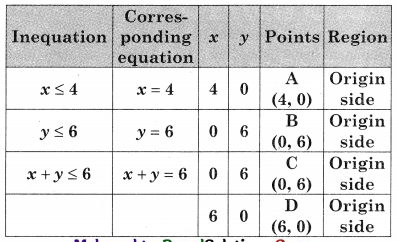
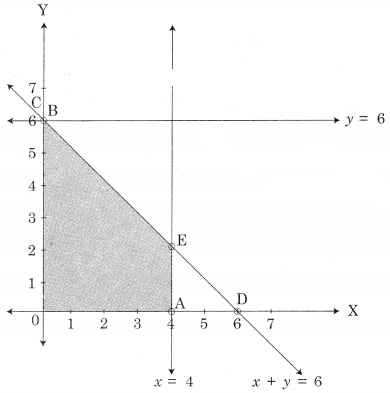
The feasible solution is AOBE
Where A(4, 0) O(0, 0) B(0, 6)
E is the point of intersection of x + y = 6 and x = 4.
∴ 4 + y = 6
∴ y = 2
∴ E = (4, 2)
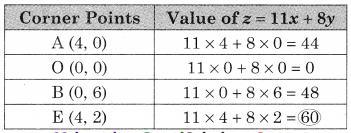
∴ z is maximum at (4, 12) and the maximum value of z = 60

Question 2.
Maximize z = 4x + 6y, Subject to 3x + 2y ≤ 12, x + y ≥ 4 x, y ≥ 0.
Solution:
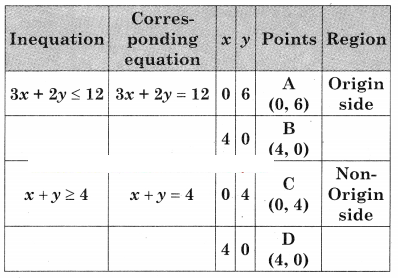
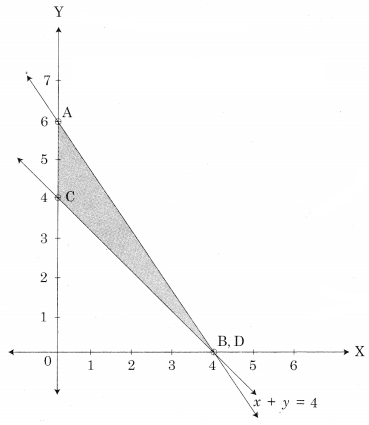
From figure, ABC is the feasible region
Where A(0, 6) B(4, 0) C(0, 4)
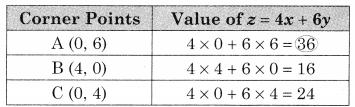
Maximum value of z = 36 at A(0, 6)
Question 3.
Maximize z = 7x + 11y, Subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solution:
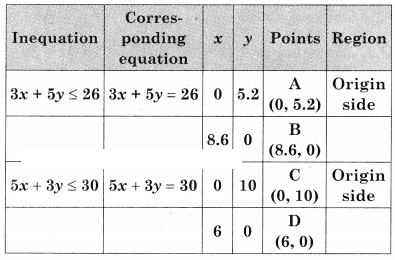
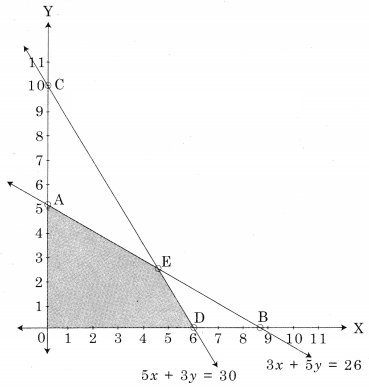
∴ AODE is the feasible region where
A(0, 5.2) O(0, 0) D(6, 0) and E is the intersection of 3x + 5y = 26 and 5x + 3y = 30
For E,
Solving 3x + 5y = 26 ……(i)
5x + 3y = 30 ……(ii)
We get, x = 4.5, y = 2.5
∴ E = (4.5, 2.5)
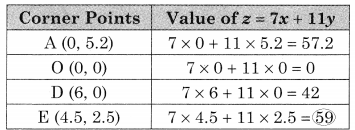
∴ Maximum value of z = 59 at E(4.5, 2.5)

Question 4.
Maximize z = 10x + 25y, Subject to 0 ≤ x ≤ 3, 0≤ y ≤ 3, x + y ≤ 5.
Solution:
The constraints can be written as, x ≤ 3, x ≥ 0, y ≥ 0, y ≤ 3, x + y ≤ 5
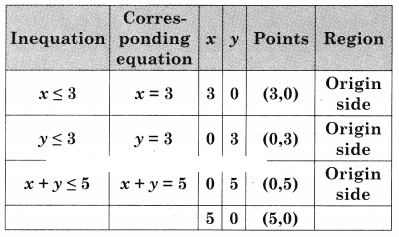
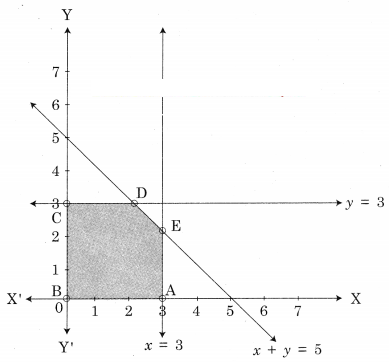
ABCDE is the feasible region where A(3, 0) B(0, 0) and C(0, 3) D is the intersection of y = 3 and x + 5y = 5 and E is the intersection of x = 3 and x + 7 = 5
For D,
Solving y = 3 ………(i)
x + y = 5 ……..(ii)
We get x = 2, y = 3
∴ D = (2, 3)
For E,
Solving x = 3 …….(i)
x + y = 5 ……….(ii)
We get x = 3, y = 2
∴ E = (3, 2)
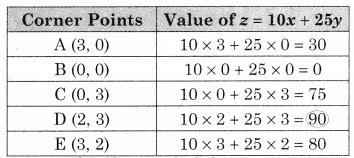
∴ Maximum value of z = 90 at D(2, 3)
Question 5.
Maximize z = 3x + 5y, Subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Solution:
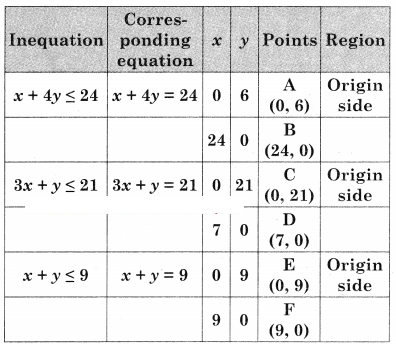
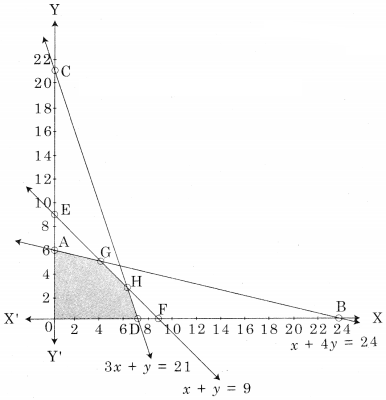
OAGHD is the feasible region where O(0, 0), A(0, 6), D(7, 0) G is the intersecting point of x + 4y = 24 and x + y = 9
H is the intersecting points of 3x + y = 21 and x + y = 9.
For G, Solving x + 4y = 24 …….(i)
x + y = 9 ………(ii)
We get, x = 4, y = 5
∴ G (4, 5)
For H, Solving x + y = 9 ………(i)
3x + y = 21 ……..(ii)
We get x = 6, y = 3
∴ H(6, 3)
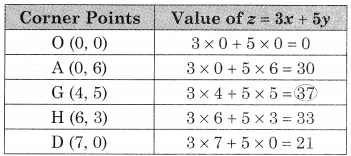
∴ Maximum value of z = 37 at the point G(4, 5)

Question 6.
Minimize z = 7x + y Subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Solution:
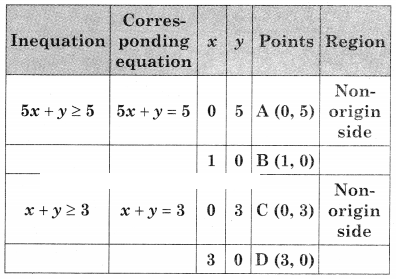
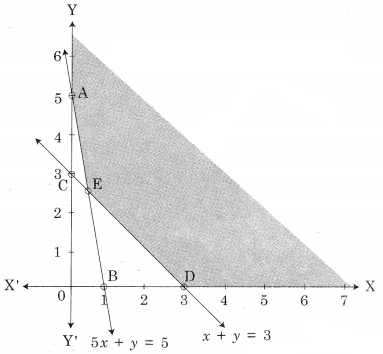
AED is the feasible region where A(0, 5) D(3, 0) and E is the point of intersection of 5x + y = 5 and x + y = 3.
For E, Solving 5x + y = 5 ………(i)
x + y = 3 ……..(ii)
We get, x = \(\frac{1}{2}\), y = \(\frac{5}{2}\)
∴ E(\(\frac{1}{2}\), \(\frac{5}{2}\))
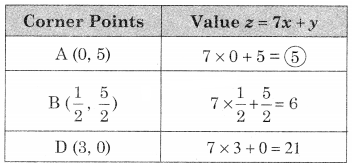
∴ Minimum value of z = 5 at A(0, 5)
Question 7.
Minimize z = 8x + 10y, Subject to 2x + y ≥ 7, 2x + 3y ≥ 15 ,y ≥ 2, x ≥ 0, y ≥ 0
Solution:
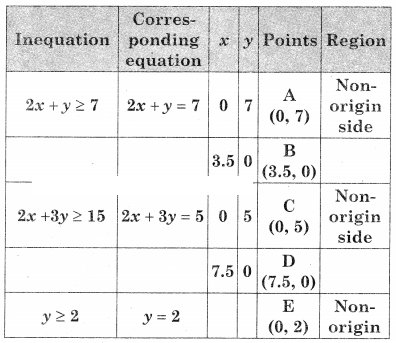
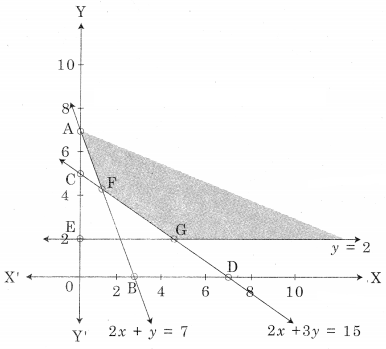
AEG is the feasible solution where A(0, 7)
F is the point of intersection of 2x + y = 7 and 2x + 3y = 15
G is the point of intersection of y = 2 and 2x + 3y = 15
For F, Solving 2x + y = 7 ……..(i)
2x + 3y = 15 ……..(ii)
We get x = \(\frac{3}{2}\), y = 4
∴ F = (\(\frac{3}{2}\), 4)
For G, Solving 2x + 3y = 15 ……..(i)
y = 2 …….(ii)
We get x = 4.5, y = 2
∴ G = (4.5, 2)
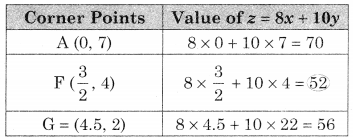
∴ Minimum value of z = 52 at F(\(\frac{3}{2}\), 4)

Question 8.
Minimize z = 6x + 2y, Subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Solution:
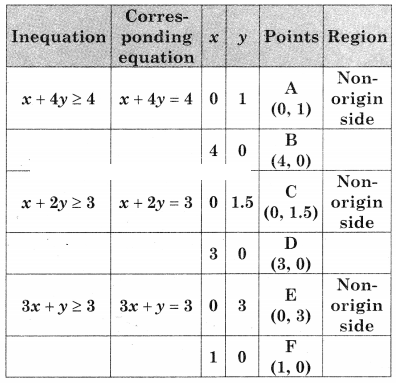
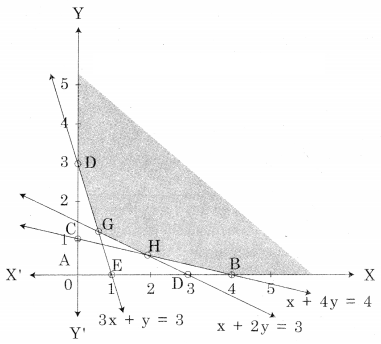
DGHB is the feasible region where D(0, 3), B(4, 0)
G is the point of intersection of 3x + y = 3 and x + 2y = 3 and H is the point of intersection of x + 2y = 3 and x + 4y = 4
For G, Solving 3x + y = 3 ……(i)
x + 2y = 3 ………(ii)
W e get x = \(\frac{3}{5}\), y = \(\frac{6}{5}\)
∴ G(\(\frac{3}{5}\), \(\frac{6}{5}\))
For H, Solving x + 2y = 3 ……..(i)
x + 4y = 4 ………(ii)
We get, x = 2, y = \(\frac{1}{2}\)
∴ H(2, \(\frac{1}{2}\))
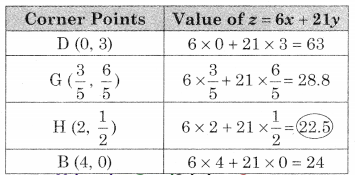
∴ Minimum value of z = 22.5 at H(2, \(\frac{1}{2}\))