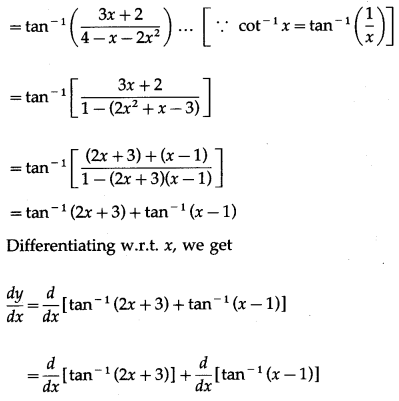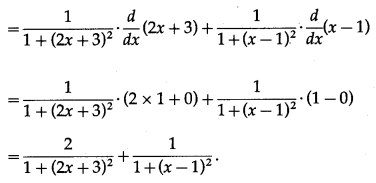Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Ex 1.2 Questions and Answers.
12th Maths Part 2 Differentiation Exercise 1.2 Questions And Answers Maharashtra Board
Question 1.
Find the derivative of the function y = f(x) using the derivative of the inverse function x = f
-1
( y) in the following
(i) y = \(\sqrt {x}\)
Solution:
y = \(\sqrt {x}\) … (1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
y
2
= x ∴ x = y
2
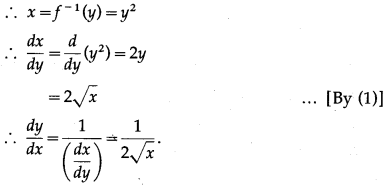
(ii) y = \(\sqrt{2-\sqrt{x}}\)
Solution:
y = \(\sqrt{2-\sqrt{x}}\) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
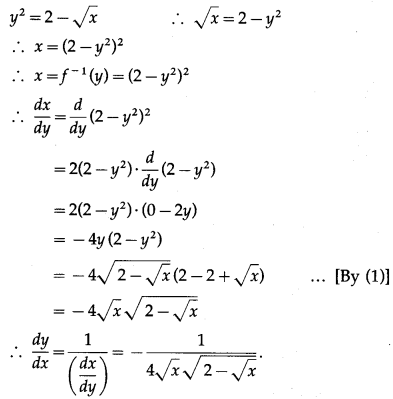
(iii) y = \(\sqrt[3]{x-2}\)
Solution:
y = \(\sqrt[3]{x-2}\) ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
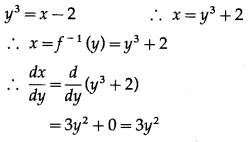
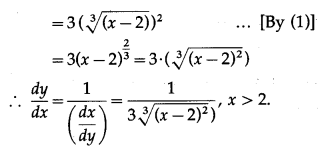

(iv) y = log (2x – 1)
Solution:
y = log (2x – 1) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
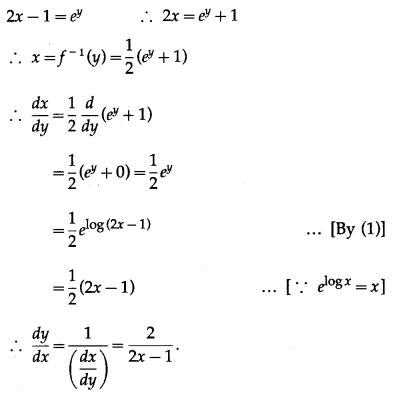
(v) y = 2x + 3
Solution:
y = 2x + 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
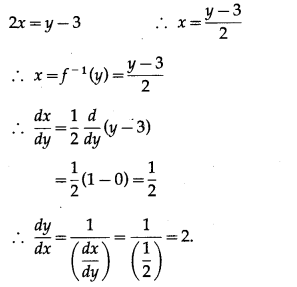
(vi) y = e
x
– 3
Solution:
y = e
x
– 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
e
x
= y + 3
∴ x = log(y + 3)
∴ x = f
-1
(y) = log(y + 3)
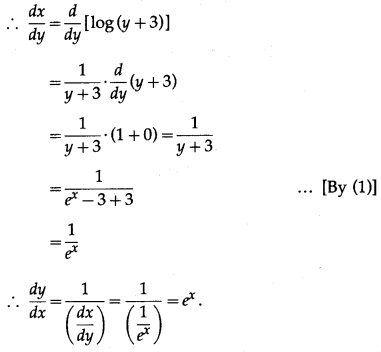

(vii) y = e
2x – 3
Solution:
y = e
2x – 3
….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
2x – 3 = log y ∴ 2x = log y + 3

(viii) y = log
2
\(\left(\frac{x}{2}\right)\)
Solution:
y = log
2
\(\left(\frac{x}{2}\right)\) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
\(\frac{x}{2}\) = 2
y
∴ x = 2∙2
y
= 2
y+1
∴ x = f
-1
(y) = 2
y+1
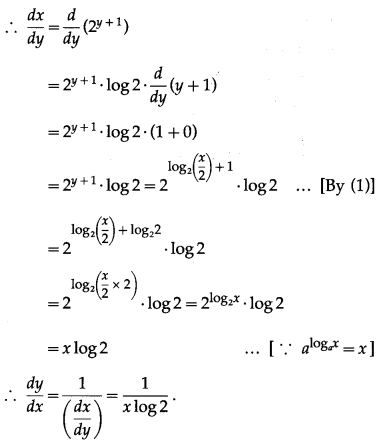
Question 2.
Find the derivative of the inverse function of
the following
(i) y = x
2
·e
x
Solution:
y = x
2
·e
x
Differentiating w.r.t. x, we get


(ii) y = x cos x
Solution:
y = x cos x
Differentiating w.r.t. x, we get
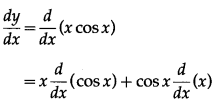
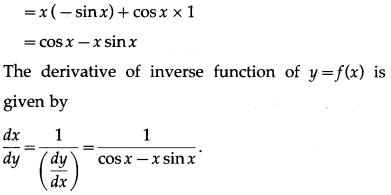
(iii) y = x·7
x
Solution:
y = x·7
x
Differentiating w.r.t. x, we get

(iv) y = x
2
+ logx
Solution:
y = x
2
+ logx
Differentiating w.r.t. x, we get


(v) y = x logx
Solution:
y = x logx
Differentiating w.r.t. x, we get
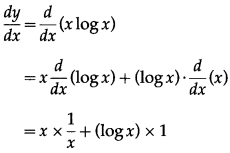

Question 3.
Find the derivative of the inverse of the following functions, and also fid their value at the points indicated against them.
(i) y = x
5
+ 2x
3
+ 3x, at x = 1
Solution:
y = x
5
+ 2x
3
+ 3x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x
5
+ 2x
3
+ 3x)
= 5x
4
+ 2 × 3x
2
+ 3 × 1
= 5x
4
+ 6x
2
+ 3
The derivative of inverse function of y = f(x) is given by
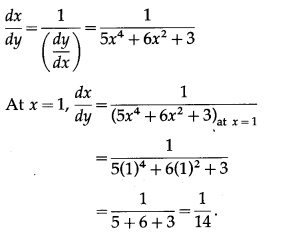
(ii) y = e
x
+ 3x + 2, at x = 0
Solution:
y = e
x
+ 3x + 2
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(e
x
+ 3x + 2)
The derivative of inverse function of y = f(x) is given by
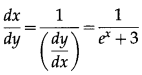
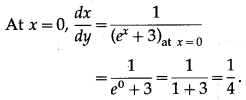

(iii) y = 3x
2
+ 2 log x
3
, at x = 1
Solution:
y = 3x
2
+ 2 log x
3
= 3x
2
+ 6 log x
Differentiating w.r.t. x, we get
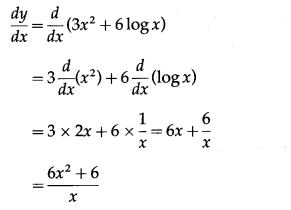
The derivative of inverse function of y = f(x) is given by
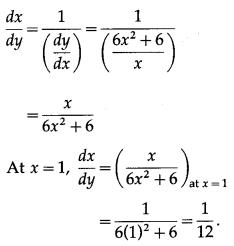
(iv) y = sin (x – 2) + x
2
, at x = 2
Solution:
y = sin (x – 2) + x
2
Differentiating w.r.t. x, we get
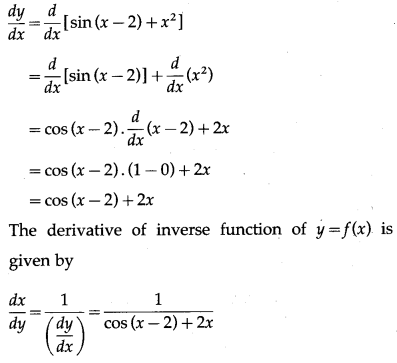
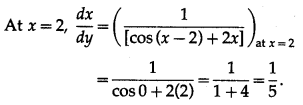
Question 4.
If f(x) = x
3
+ x – 2, find (f
-1
)’ (0).
Question is modified.
If f(x) = x
3
+ x – 2, find (f
-1
)’ (-2).
Solution:
f(x) = x
3
+ x – 2 ….(1)
Differentiating w.r.t. x, we get


Question 5.
Using derivative prove
(i) tan
-1
x + cot
-1
x = \(\frac{\pi}{2}\)
Solution:
let f(x) = tan
-1
x + cot
-1
x
Differentiating w.r.t. x, we get
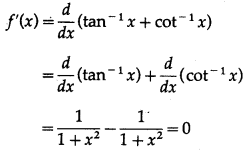
Since, f'(x) = 0, f(x) is a constant function.
Let f(x) = k.
For any value of x, f(x) = k
Let x = 0.
Then f(0) = k ….(2)
From (1), f(0) = tan
-1
(0) + cot
-1
(0)
= 0 + \(\frac{\pi}{2}=\frac{\pi}{2}\)
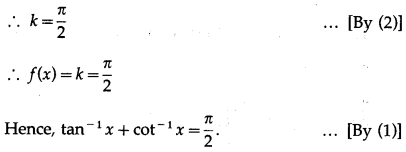
(ii) sec
-1
x + cosec
-1
x = \(\frac{\pi}{2}\) . . . [for |x| ≥ 1]
Solution:
Let f(x) = sec
-1
x + cosec
-1
x for |x| ≥ 1 ….(1)
Differentiating w.r.t. x, we get
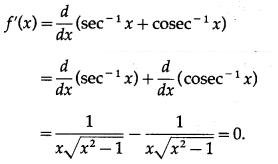
Since, f'(x) = 0, f(x) is a constant function.
Let f(x) = k.
For any value of x, f(x) = k, where |x| > 1
Let x = 2.
Then, f(2) = k ……(2)
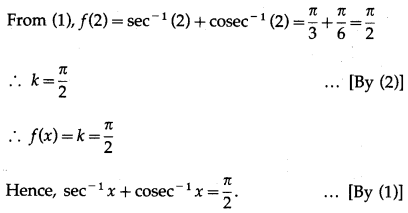

Question 6.
Diffrentiate the following w. r. t. x.
(i) tan
-1
(log x)
Solution:
Let y = tan
-1
(log x)
Differentiating w.r.t. x, we get
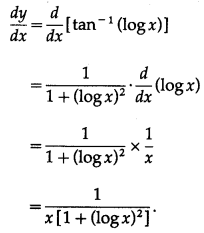
(ii) cosec
-1
(e
-x
)
Solution:
Let y = cosec
-1
(e
-x
)
Differentiating w.r.t. x, we get
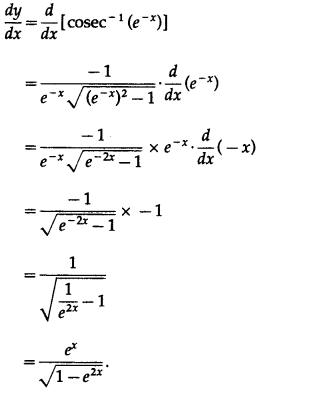
(iii) cot
-1
(x
3
)
Solution:
Let y = cot
-1
(x
3
)
Differentiating w.r.t. x, we get
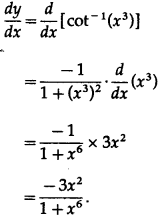

(iv) cot
-1
(4
x
Solution:
Let y = cot
-1
(4
x
Differentiating w.r.t. x, we get
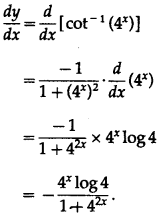
(v) tan
-1
(\(\sqrt {x}\))
Solution:
Let y = tan
-1
(\(\sqrt {x}\))
Differentiating w.r.t. x, we get
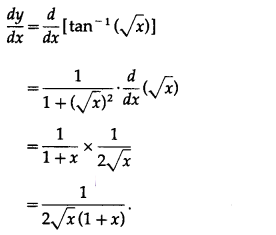
(vi) sin
-1
\(\left(\sqrt{\frac{1+x^{2}}{2}}\right)\)
Solution:
Let y = sin
-1
\(\left(\sqrt{\frac{1+x^{2}}{2}}\right)\)
Differentiating w.r.t. x, we get
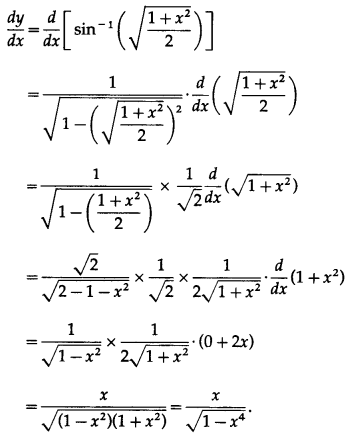

(vii) cos
-1
(1 – x
2
)
Solution:
Let y = cos
-1
(1 – x
2
)
Differentiating w.r.t. x, we get
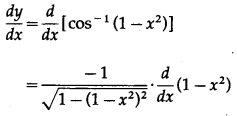
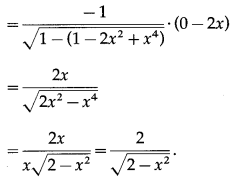
(viii) sin
-1
\(\left(x^{\frac{3}{2}}\right)\)
Solution:
Let y = sin
-1
\(\left(x^{\frac{3}{2}}\right)\)
Differentiating w.r.t. x, we get
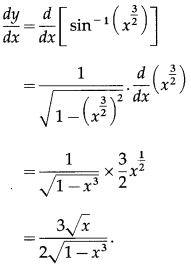

(ix) cos
3
[cos
-1
(x
3
)]
Solution:
Let y = cos
3
[cos
-1
(x
3
)]
= [cos(cos
-1
x
3
)]
3
= (x
3
)
3
= x
9
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x
9
) = 9x
8
.
(x) sin
4
[sin
-1
(\(\sqrt {x}\))]
Solution:
Let y = sin
4
[sin
-1
(\(\sqrt {x}\))]
= {sin[sin
-1
(\(\sqrt {x}\))]}
8
= (\(\sqrt {x}\))
4
= x
2
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x
2
) = 2x.
Question 7.
Diffrentiate the following w. r. t. x.
(i) cot
-1
[cot (e
x2
)]
Solution:
Let y = cot
-1
[cot (e
x2
)] = e
x2
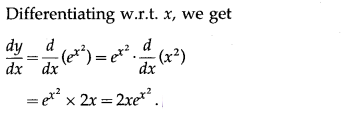

(ii) cosec
-1
\(\left(\frac{1}{\cos \left(5^{x}\right)}\right)\)
Solution:
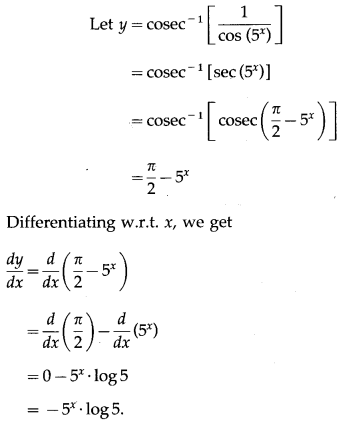
(iii) cos
-1
\(\left(\sqrt{\frac{1+\cos x}{2}}\right)\)
Solution:

(iv) cos
-1
\(\left(\sqrt{\frac{1-\cos \left(x^{2}\right)}{2}}\right)\)
Solution:

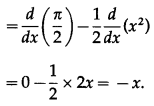
(v) tan
-1
\(\left(\frac{1-\tan \left(\frac{x}{2}\right)}{1+\tan \left(\frac{x}{2}\right)}\right)\)
Solution:

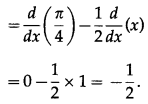

(vi) cosec
-1
\(\left(\frac{1}{4 \cos ^{3} 2 x-3 \cos 2 x}\right)\)
Solution:

(vii) tan
-1
\(\left(\frac{1+\cos \left(\frac{x}{3}\right)}{\sin \left(\frac{x}{3}\right)}\right)\)
Solution:
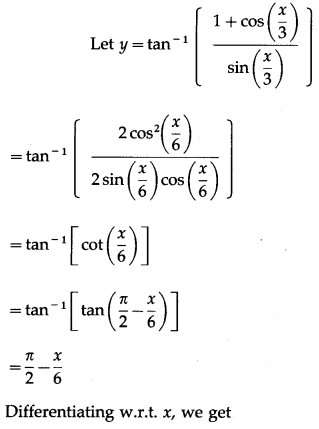
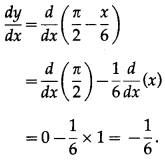
(viii) cot
-1
\(\left(\frac{\sin 3 x}{1+\cos 3 x}\right)\)
Solution:
Let y = cot
-1
\(\left(\frac{\sin 3 x}{1+\cos 3 x}\right)\)
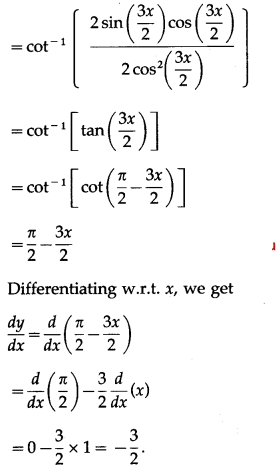

(ix) tan
-1
\(\left(\frac{\cos 7 x}{1+\sin 7 x}\right)\)
Solution:
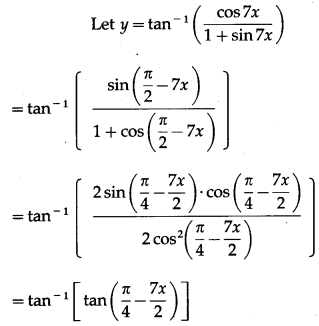
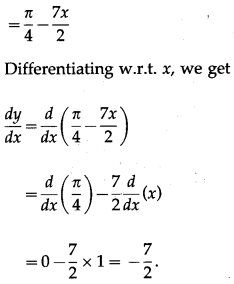
(x) tan
-1
\(\left(\sqrt{\frac{1+\cos x}{1-\cos x}}\right)\)
Solution:
Let y = tan
-1
\(\left(\sqrt{\frac{1+\cos x}{1-\cos x}}\right)\)

(xi) tan
-1
(cosec x + cot x)
Solution:
Let y = tan
-1
(cosec x + cot x)
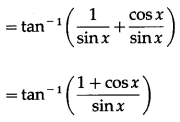
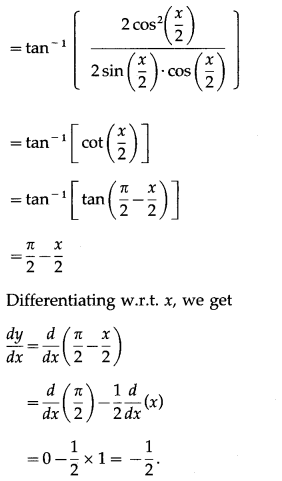

(xii) cot
-1
\(\left(\frac{\sqrt{1+\sin \left(\frac{4 x}{3}\right)}+\sqrt{1-\sin \left(\frac{4 x}{3}\right)}}{\sqrt{1+\sin \left(\frac{4 x}{3}\right)}-\sqrt{1-\sin \left(\frac{4 x}{3}\right)}}\right)\)
Solution:
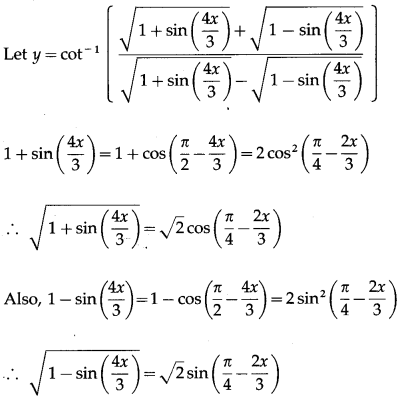
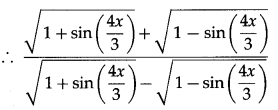
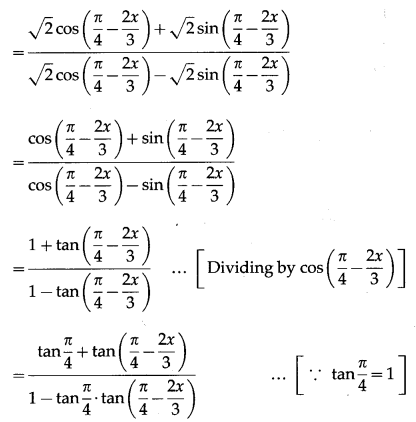
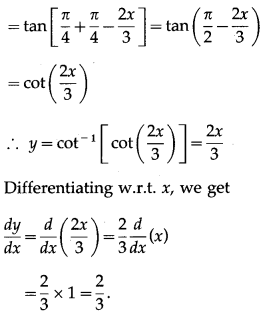
Question 8.
(i)
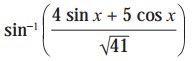
Solution:
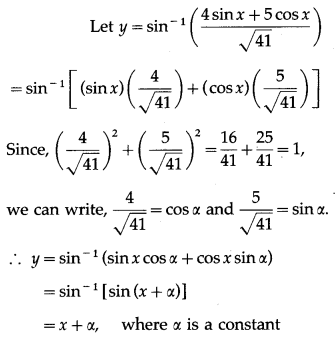
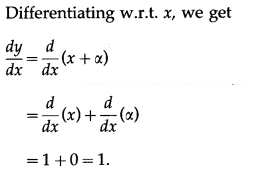
(ii)
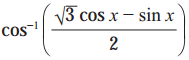
Solution:

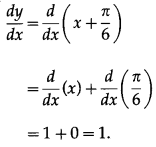

(iii)
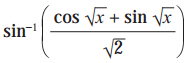
Solution:
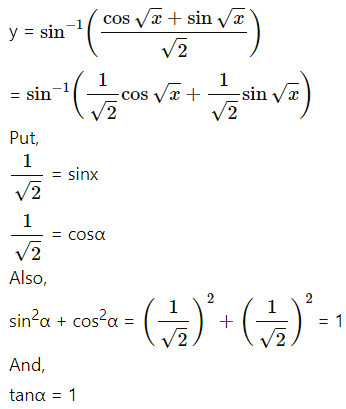
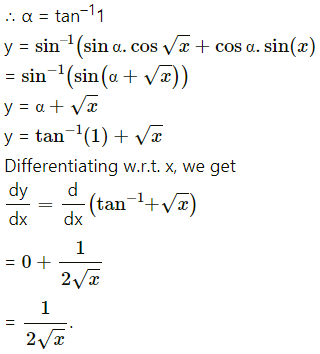
(iv)
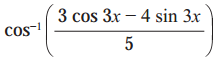
Solution:
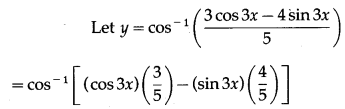
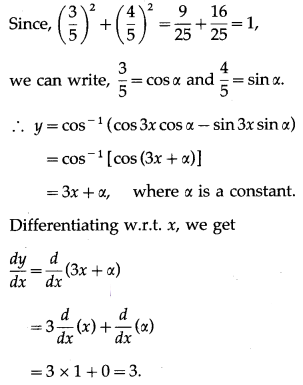
(v)
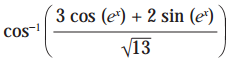
Solution:
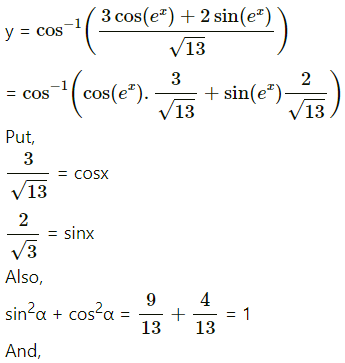
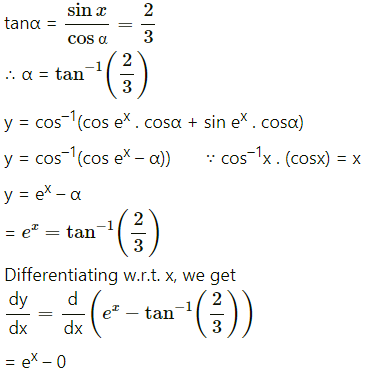
= e
x
.

(vi)
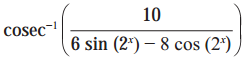
Solution:
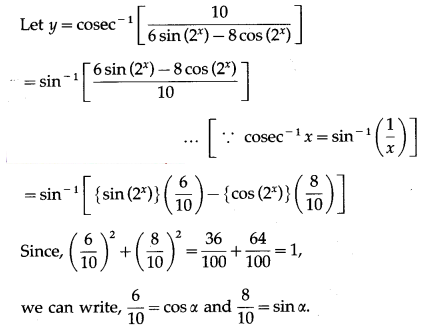
y = sin
-1
[sin(2
x
)∙cosα – cos(2
x
)∙sinα]
= sin
–
[sin(2
x
– α)]
= 2
x
– α, where α is a constant
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(2
x
– α)
= \(\frac{d}{d x}\)(2
x
) – \(\frac{d}{d x}\)(α)
= 2
x
∙log2 – 0
= 2
x
∙log2
Question 9.
Diffrentiate the following w. r. t. x.
(i) cos
-1
\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
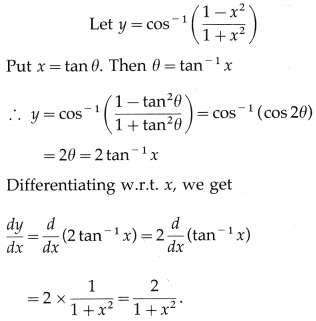
(ii) tan
-1
\(\left(\frac{2 x}{1-x^{2}}\right)\)
Solution:
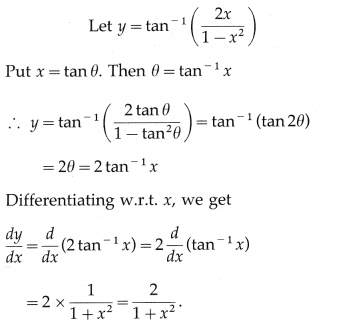

(iii) sin
-1
\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
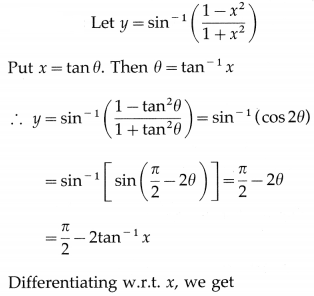
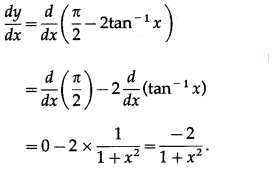
(iv) sin
-1
(2x\(\sqrt{1-x^{2}}\))
Solution:
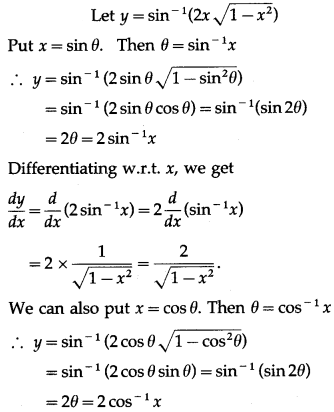
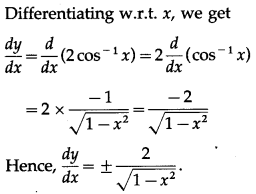
(v) cos
-1
(3x – 4x
3
)
Solution:
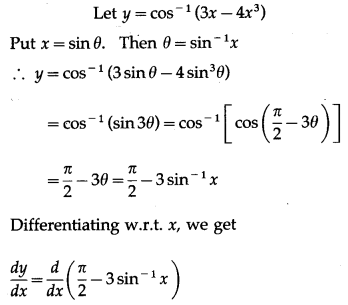
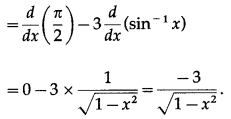
(vi) cos
-1
\(\left(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\right)\)
Solution:
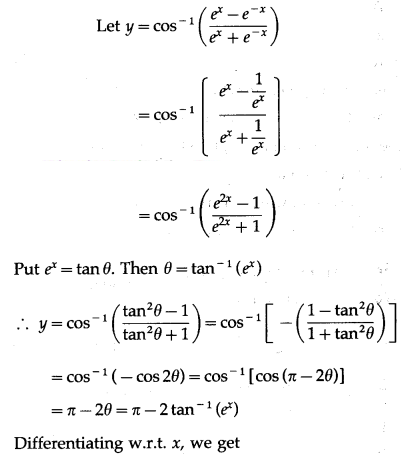
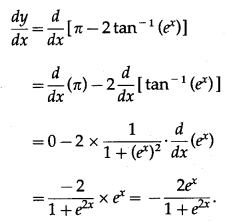

(vii) cos
-1
\(\left(\frac{1-9^{x}}{1+9^{x}}\right)\)
Solution:
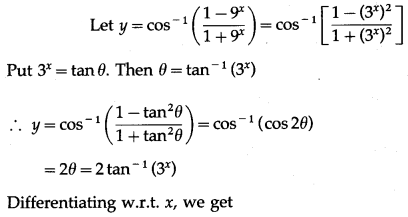
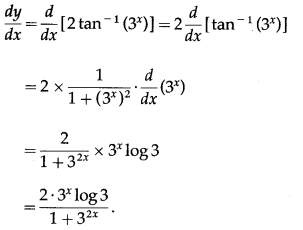
(viii) sin
-1
\(\left(\frac{4^{x+\frac{1}{2}}}{1+2^{4 x}}\right)\)
Solution:

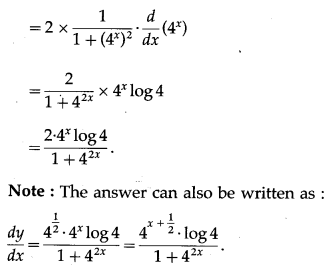
(ix) sin
-1
\(\left(\frac{1-25 x^{2}}{1+25 x^{2}}\right)\)
Solution:
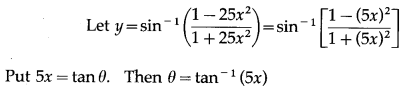
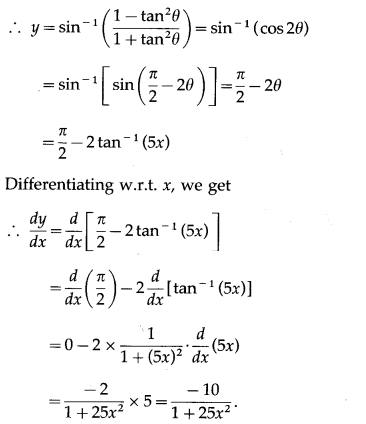
(x) sin
-1
\(\left(\frac{1-x^{3}}{1+x^{3}}\right)\)
Solution:
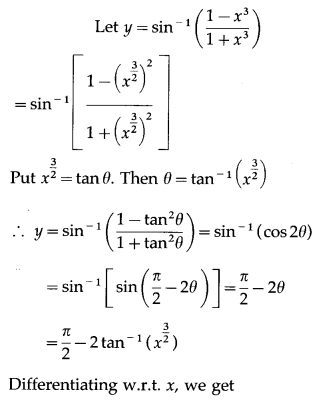
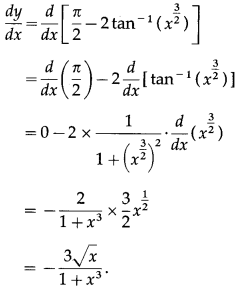

(xi) tan
-1
\(\left(\frac{2 x^{\frac{5}{2}}}{1-x^{5}}\right)\)

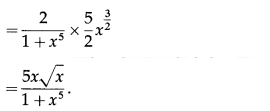
(xii) cot
-1
\(\left(\frac{1-\sqrt{x}}{1+\sqrt{x}}\right)\)
Solution:
Let y = cot
-1
\(\left(\frac{1-\sqrt{x}}{1+\sqrt{x}}\right)\)
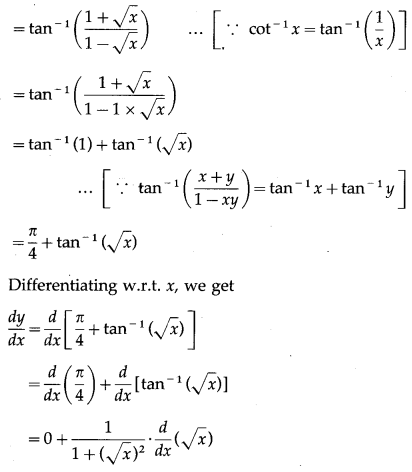
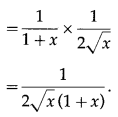
Question 10.
Diffrentiate the following w. r. t. x.
(i) tan
-1
\(\left(\frac{8 x}{1-15 x^{2}}\right)\)
Solution:
Let y = tan
-1
\(\left(\frac{8 x}{1-15 x^{2}}\right)\)


(ii) cot
-1
\(\left(\frac{1+35 x^{2}}{2 x}\right)\)
Solution:
Let y = cot
-1
\(\left(\frac{1+35 x^{2}}{2 x}\right)\)

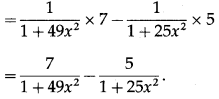
(iii) tan
-1
\(\left(\frac{2 \sqrt{x}}{1+3 x}\right)\)
Solution:
Let y = tan
-1
\(\left(\frac{2 \sqrt{x}}{1+3 x}\right)\)
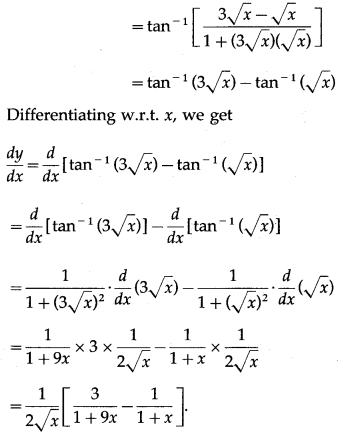
(iv) tan
-1
\(\left(\frac{2^{x+2}}{1-3\left(4^{x}\right)}\right)\)
Solution:
Let y = tan
-1
\(\left(\frac{2^{x+2}}{1-3\left(4^{x}\right)}\right)\)
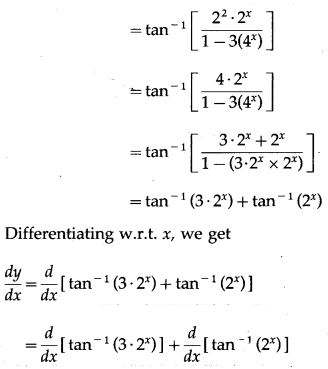
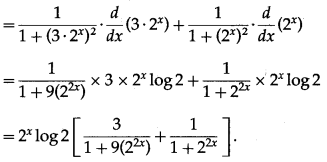

(v) tan
-1
\(\left(\frac{2^{x}}{1+2^{2 x+1}}\right)\)
Solution:
Let y = tan
-1
\(\left(\frac{2^{x}}{1+2^{2 x+1}}\right)\)
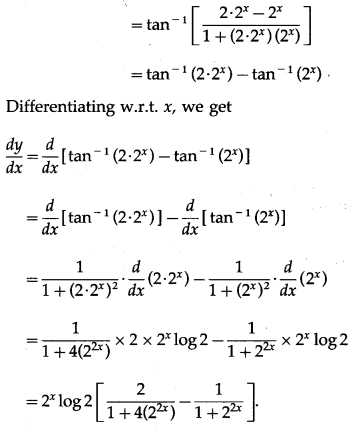
(vi) cot
-1
\(\left(\frac{a^{2}-6 x^{2}}{5 a x}\right)\)
Solution:
Let y = cot
-1
\(\left(\frac{a^{2}-6 x^{2}}{5 a x}\right)\)

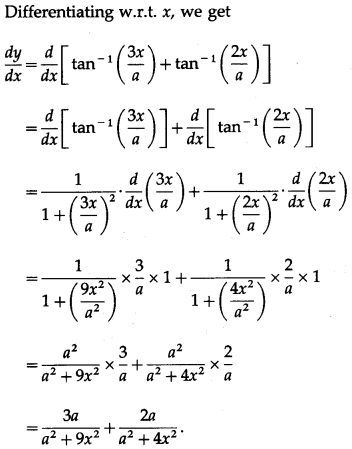
(vii) tan
-1
\(\left(\frac{a+b \tan x}{b-a \tan x}\right)\)
Solution:
Let y = tan
-1
\(\left(\frac{a+b \tan x}{b-a \tan x}\right)\)


(viii) tan
-1
\(\left(\frac{5-x}{6 x^{2}-5 x-3}\right)\)
Solution:
Let y = tan
-1
\(\left(\frac{5-x}{6 x^{2}-5 x-3}\right)\)
= tan
-1
\(\left[\frac{5-x}{1+\left(6 x^{2}-5 x-4\right)}\right]\)
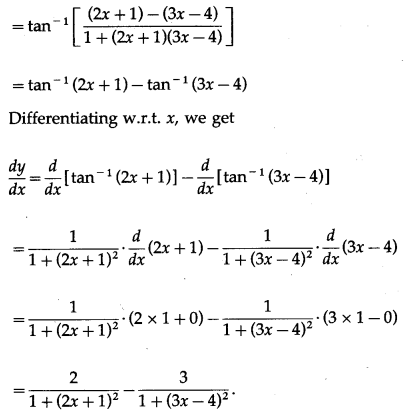
(ix) cot
-1
\(\left(\frac{4-x-2 x^{2}}{3 x+2}\right)\)
Solution:
Let y = cot
-1
\(\left(\frac{4-x-2 x^{2}}{3 x+2}\right)\)