Differentiation Class 12 Maths 2 Exercise 1.4 Solutions Maharashtra Board

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Ex 1.4 Questions and Answers.

12th Maths Part 2 Differentiation Exercise 1.4 Questions And Answers Maharashtra Board

Question 1.
Find \(\frac{d y}{d x}\) if
(i) x = at ² , y = 2at
Solution:
x = at ² , y = 2at
Differentiating x and y w.r.t. t, we get

(ii) x = a cot θ, y = b cosec θ
Solution:
x = a cot θ, y = b cosec θ
Differentiating x and y w.r.t. θ, we get

(iii) x = \(\sqrt{a^{2}+m^{2}}\), y = log (a ² + m ² )
Solution:
x = \(\sqrt{a^{2}+m^{2}}\), y = log (a ² + m ² )
Differentiating x and y w.r.t. m, we get
\(\frac{d x}{d m}=\frac{d}{d m}\left(\sqrt{a^{2}+m^{2}}\right)\)

(iv) x = sin θ, y = tan θ
Solution:
x = sin θ, y = tan θ
Differentiating x and y w.r.t. θ, we get

(v) x = a(1 – cos θ), y = b(θ – sin θ)
Solution:
x = a(1 – cos θ), y = b(θ – sin θ)
Differentiating x and y w.r.t. θ, we get

(vi) x = \(\left(t+\frac{1}{t}\right)^{a}\), y = \(a^{t+\frac{1}{t}}\), where a > 0, a ≠ 1 and t ≠ 0
Solution:
x = \(\left(t+\frac{1}{t}\right)^{a}\), y = \(a^{t+\frac{1}{t}}\) ………(1)
Differentiating x and y w.r.t. t, we get

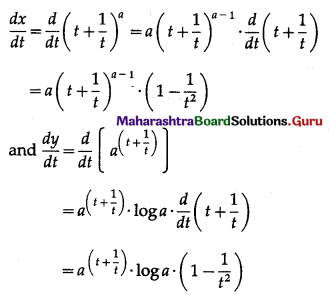
(vii) x = \(\cos ^{-1}\left(\frac{2 t}{1+t^{2}}\right)\), y = \(\sec ^{-1}\left(\sqrt{1+t^{2}}\right)\)
Solution:
x = \(\cos ^{-1}\left(\frac{2 t}{1+t^{2}}\right)\), y = \(\sec ^{-1}\left(\sqrt{1+t^{2}}\right)\)
Put t = tan θ Then θ = tan ^-1 t

(viii) x = cos ^-1 (4t ³ – 3t), y = \(\tan ^{-1}\left(\frac{\sqrt{1-t^{2}}}{t}\right)\)
Solution:
x = cos ^-1 (4t ³ – 3t), y = \(\tan ^{-1}\left(\frac{\sqrt{1-t^{2}}}{t}\right)\)
Put t = cos θ. Then θ = cos ^-1 t
x = cos ^-1 (4cos ³ θ – 3cos θ)

Question 2.
Find \(\frac{d y}{d x}\), if
(i) x = cosec ² θ, y = cot ³ θ at θ = \(\frac{\pi}{6}\)
Solution:
x = cosec ² θ, y = cot ³ θ
Differentiating x and y w.r.t. θ, we get

(ii) x = a cos ³ θ, y = a sin ³ θ at θ = \(\frac{\pi}{3}\)
Solution:
x = a cos ³ θ, y = a sin ³ θ
Differentiating x and y w.r.t. θ, we get

(iii) x = t ² + t + 1, y = sin(\(\frac{\pi t}{2}\)) + cos(\(\frac{\pi t}{2}\)) at t = 1
Solution:
x = t ² + t + 1, y = sin(\(\frac{\pi t}{2}\)) + cos(\(\frac{\pi t}{2}\))
Differentiating x and y w.r.t. t, we get

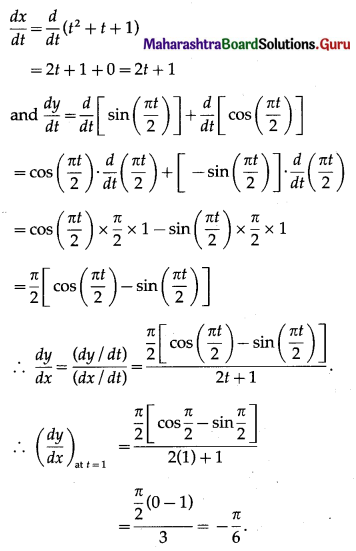
(iv) x = 2 cos t + cos 2t, y = 2 sin t – sin 2t at t = \(\frac{\pi}{4}\)
Solution:
x = 2 cos t + cos 2t, y = 2 sin t – sin 2t
Differentiating x and y w.r.t. t, we get

(v) x = t + 2 sin(πt), y = 3t – cos(πt) at t = \(\frac{1}{2}\)
Solution:
x = t + 2 sin(πt), y = 3t – cos(πt)
Differentiating x and y w.r.t. t, we get

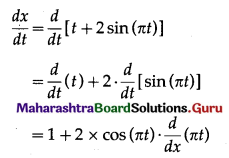
Question 3.
(i) If x = \(a \sqrt{\sec \theta-\tan \theta}\), y = \(a \sqrt{\sec \theta+\tan \theta}\), then show that \(\frac{d y}{d x}=-\frac{y}{x}\)
Solution:
x = \(a \sqrt{\sec \theta-\tan \theta}\), y = \(a \sqrt{\sec \theta+\tan \theta}\)

(ii) If x = \(e^{\sin 3 t}\), y = \(e^{\cos 3 t}\), then show that \(\frac{d y}{d x}=-\frac{y \log x}{x \log y}\)
Solution:
x = \(e^{\sin 3 t}\), y = \(e^{\cos 3 t}\)
log x = log \(e^{\sin 3 t}\), log y = log \(e^{\cos 3 t}\)
log x = (sin 3t)(log e), log y = (cos 3t)(log e)
log x = sin 3t, log y = cos 3t ….. (1) [∵ log e = 1]
Differentiating both sides w.r.t. t, we get

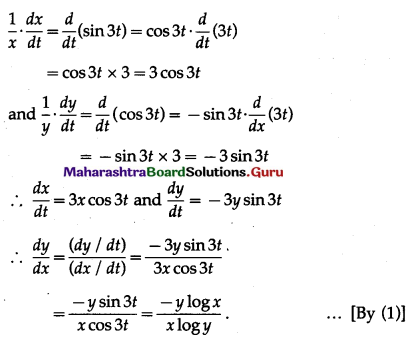
(iii) If x = \(\frac{t+1}{t-1}\), y = \(\frac{1-t}{t+1}\), then show that y2 – \(\frac{d y}{d x}\) = 0.
Solution:
x = \(\frac{t+1}{t-1}\), y = \(\frac{1-t}{t+1}\)

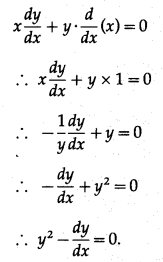
(iv) If x = a cos ³ t, y = a sin ³ t, then show that \(\frac{d y}{d x}=-\left(\frac{y}{x}\right)^{\frac{1}{3}}\)
Solution:
x = a cos ³ t, y = a sin ³ t
Differentiating x and y w.r.t. t, we get

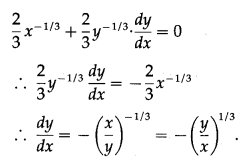
(v) If x = 2 cos ⁴ (t + 3), y = 3 sin ⁴ (t + 3), show that \(\frac{d y}{d x}=-\sqrt{\frac{3 y}{2 x}}\)
Solution:
x = 2 cos ⁴ (t + 3), y = 3 sin ⁴ (t + 3)

(vi) If x = log (1 + t ² ), y = t – tan ^-1 t, show that \(\frac{d y}{d x}=\frac{\sqrt{e^{x}-1}}{2}\)
Solution:
x = log (1 + t ² ), y = t – tan ^-1 t
Differentiating x and y w.r.t. t, we get

(vii) If x = \(\sin ^{-1}\left(e^{t}\right)\), y = \(\sqrt{1-e^{2 t}}\), show that sin x + \(\frac{d y}{d x}\) = 0
Solution:
x = \(\sin ^{-1}\left(e^{t}\right)\), y = \(\sqrt{1-e^{2 t}}\)
Differentiating x and y w.r.t. t, we get

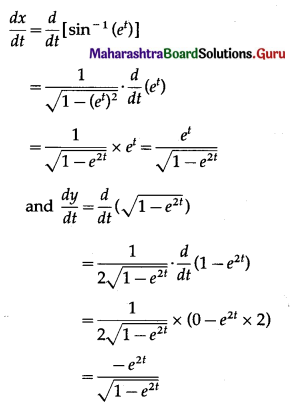
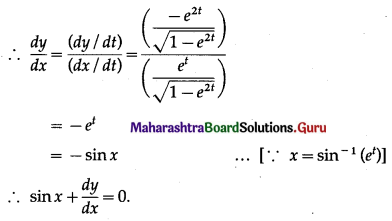
(viii) If x = \(\frac{2 b t}{1+t^{2}}\), y = \(a\left(\frac{1-t^{2}}{1+t^{2}}\right)\), show that \(\frac{d x}{d y}=-\frac{b^{2} y}{a^{2} x}\)
Solution:
x = \(\frac{2 b t}{1+t^{2}}\), y = \(a\left(\frac{1-t^{2}}{1+t^{2}}\right)\)

Question 4.
(i) Differentiate x sin x w.r.t tan x.
Solution:
Let u = x sinx and v = tan x
Then we want to find \(\frac{d u}{d v}\)
Differentiating u and v w.r.t. x, we get

(ii) Differentiate \(\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)\) w.r.t \(\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
Let u = \(\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)\) and v = \(\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Then we want to find \(\frac{d u}{d v}\)

(iii) Differentiate \(\tan ^{-1}\left(\frac{x}{\sqrt{1-x^{2}}}\right)\) w.r.t \(\sec ^{-1}\left(\frac{1}{2 x^{2}-1}\right)\)
Solution:

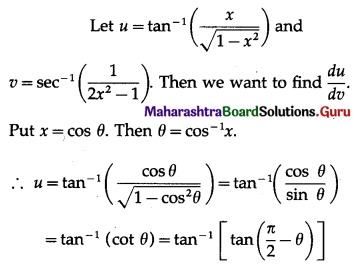
(iv) Differentiate \(\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)\) w.r.t. tan ^-1 x
Solution:
Let u = \(\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)\) and v = tan ^-1 x
Then we want to find \(\frac{d u}{d v}\)
Put x = tan θ. Then θ = tan ^-1 x.

(v) Differentiate 3x w.r.t. log _x 3.
Solution:
Let u = 3x and v = log _x 3.
Then we want to find \(\frac{d u}{d v}\)
Differentiating u and v w.r.t. x, we get
\(\frac{d u}{d x}=\frac{d}{d x}\left(3^{x}\right)=3^{x} \cdot \log 3\)

(vi) Differentiate \(\tan ^{-1}\left(\frac{\cos x}{1+\sin x}\right)\) w.r.t. sec ^-1 x.
Solution:
Let u = \(\tan ^{-1}\left(\frac{\cos x}{1+\sin x}\right)\) and v = sec ^-1 x
Then we want to find \(\frac{d u}{d v}\).
Differentiating u and v w.r.t. x, we get

(vii) Differentiate x ^x w.r.t. x ^{sin x} .
Solution:
Let u = x ^x and v = x ^{sin x}
Then we want to find \(\frac{d u}{d x}\).
Take, u = x ^x
log u = log x ^x = x log x
Differentiating both sides w.r.t. x, we get

(viii) Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) w.r.t. \(\tan ^{-1}\left(\frac{2 x \sqrt{1-x^{2}}}{1-2 x^{2}}\right)\)
Solution:
Let u = \(\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) and v = \(\tan ^{-1}\left(\frac{2 x \sqrt{1-x^{2}}}{1-2 x^{2}}\right)\)
Then we want to find \(\frac{d u}{d v}\)
u = \(\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\)
Put x = tan θ. Then θ = tan ^-1 x and