Matrices Class 12 Maths 1 Exercise 2.1 Solutions Maharashtra Board

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Ex 2.1 Questions and Answers.

12th Maths Part 1 Matrices Exercise 2.1 Questions And Answers Maharashtra Board

Question 1.
Apply the given elementary transformation on each of the following matrices.
A = \(\left[\begin{array}{cc}
1 & 0 \\
-1 & 3
\end{array}\right]\), R ₁ ↔ R ₂
Solution:
A = \(\left[\begin{array}{cc}
1 & 0 \\
-1 & 3
\end{array}\right]\)
By R ₁ ↔ R ₂ , we get,
A ~ \(\left[\begin{array}{rr}
-1 & 3 \\
1 & 0
\end{array}\right]\)

Question 2.
B = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 5 & 4
\end{array}\right]\), R ₁ → R ₁ → R ₂
Solution:
B = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 5 & 4
\end{array}\right]\),
R ₁ → R ₁ → R ₂ gives,
B ~ \(\left[\begin{array}{rrr}
-1 & -6 & -1 \\
2 & 5 & 4
\end{array}\right]\)

Question 3.
A = \(\left[\begin{array}{ll}
5 & 4 \\
1 & 3
\end{array}\right]\), C ₁ ↔ C ₂ ; B = \(\left[\begin{array}{ll}
3 & 1 \\
4 & 5
\end{array}\right]\), R ₁ ↔ R ₂ . What do you observe?
Solution:
A = \(\left[\begin{array}{ll}
5 & 4 \\
1 & 3
\end{array}\right]\)
By C ₁ ↔ C ₂ , we get,
A ~ \(\left[\begin{array}{ll}
4 & 5 \\
3 & 1
\end{array}\right]\) …(1)
B = \(\left[\begin{array}{ll}
3 & 1 \\
4 & 5
\end{array}\right]\)
By R ₁ ↔ R ₂ , we get,
B ~ \(\left[\begin{array}{ll}
4 & 5 \\
3 & 1
\end{array}\right]\) …(2)
From (1) and (2), we observe that the new matrices are equal.

Question 4.
A = \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & 1 & 3
\end{array}\right]\), 2C ₂
B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 4 & 5
\end{array}\right]\), -3R ₁
Find the addition of the two new matrices.
Solution:
A = \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & 1 & 3
\end{array}\right]\)
By 2C ₂ , we get,
A ~ \(\left[\begin{array}{rrr}
1 & 4 & -1 \\
0 & 2 & 3
\end{array}\right]\)
B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 4 & 5
\end{array}\right]\)
By -3R ₁ , we get,
B ~ \(\left[\begin{array}{rrr}
-3 & 0 & -6 \\
2 & 4 & 5
\end{array}\right]\)
Now, addition of the two new matrices

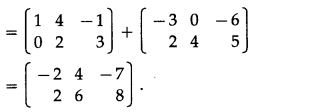
Question 5.
A = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\), 3R ₃ and then C ₃ + 2C ₂ .
Solution:
A = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\)
By 3R ₃ , we get
A ~ \(\left[\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
9 & 9 & 3
\end{array}\right]\)
By C ₃ + 2C ₂ , we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 3+2(-1) \\
2 & 1 & 0+2(1) \\
9 & 9 & 3+2(9)
\end{array}\right)\)
∴ A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
9 & 9 & 21
\end{array}\right)\)

Question 6.
A = \(\left(\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right)\), C ₃ + 2C ₂ and then 3R ₃ . What do you conclude from Ex. 5 and Ex. 6 ?
Solution:
A = \(\left(\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right)\)
By C ₃ + 2C ₂ , we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 3+2(-1) \\
2 & 1 & 0+2(1) \\
3 & 3 & 1+2(3)
\end{array}\right)\)
∴ A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
3 & 3 & 7
\end{array}\right)\)
By 3R ₃ , we get
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
9 & 9 & 21
\end{array}\right)\)
We conclude from Ex. 5 and Ex. 6 that the matrix remains same by interchanging the order of the elementary transformations. Hence, the transformations are commutative.

Question 7.
Use suitable transformation on \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\) into an upper triangular matrix.
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
By R ₂ – 3R ₁ , we get,
A ~ \(\left[\begin{array}{rr}
1 & 2 \\
0 & -2
\end{array}\right]\)
This is an upper triangular matrix.

Question 8.
Convert \(\left[\begin{array}{rr}
1 & -1 \\
2 & 3
\end{array}\right]\) into an identity matrix by suitable row transformations.
Solution:
Let A = \(\left[\begin{array}{rr}
1 & -1 \\
2 & 3
\end{array}\right]\)
By R ₂ – 2R ₁ , we get,
A ~ \(\left[\begin{array}{rr}
1 & -1 \\
0 & 5
\end{array}\right]\)
By \(\left(\frac{1}{5}\right)\)R ₂ , we get,
A ~ \(\left[\begin{array}{rr}
1 & -1 \\
0 & 1
\end{array}\right]\)
By R ₁ + R ₂ , we get,
A ~ \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
This is an identity matrix.

Question 9.
Transform \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 1 & 3 \\
3 & 2 & 4
\end{array}\right]\) into an upper triangular matrix by suitable row transformations.
Solution:
Let A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 1 & 3 \\
3 & 2 & 4
\end{array}\right]\)
By R ₂ – 2R ₁ and R ₃ – 3R ₁ , we get
A ~ \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
0 & 3 & -1 \\
0 & 5 & -2
\end{array}\right]\)
By R ₃ – \(\left(\frac{5}{3}\right)\)R ₂ , we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 2 \\
0 & 3 & -1 \\
0 & 0 & -\frac{1}{3}
\end{array}\right)\)
This is an upper triangular matrix.