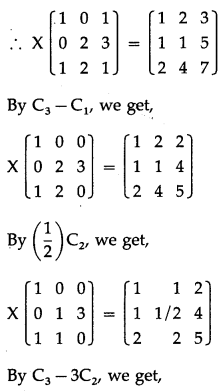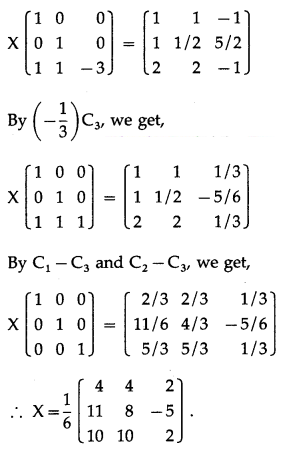Matrices Class 12 Maths 1 Miscellaneous Exercise 2A Solutions Maharashtra Board

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Miscellaneous Exercise 2A Questions and Answers.

12th Maths Part 1 Matrices Miscellaneous Exercise 2A Questions And Answers Maharashtra Board

Question 1.
If A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\) then reduce it to I ₃ by using column transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right|\)
= 1(1 – 0) – 0 + 0 = 1 ≠ 0
∴ A is a non-singular matrix.
Hence, the required transformation is possible.
Now, A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\)
By C ₁ – 2C ₂ , we get, A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
-3 & 3 & 1
\end{array}\right]\)
By C ₁ + 3C ₃ and C ₂ – 3C ₃ , we get,
A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) = I ₃ .

Question 2.
If A = \(\left[\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right]\), then reduce it to I ₃ by using row transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right|\)
= 2 (0 – 1) – 1(1 – 1) + 3 (1 – 0)
= -2 – 0 + 3 = 1 ≠ 0
∴ A is a non-singular matrix.
Hence, the required transformation is possible.
Now, A = \(\left[\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right]\)
By R ₁ – R ₂ , we get,

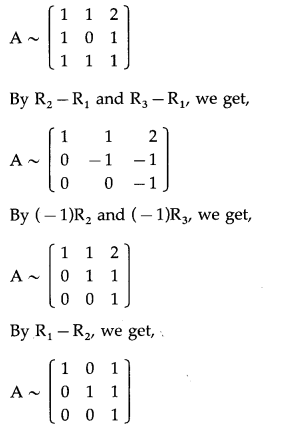
By R ₁ – R ₃ and By R ₂ – R ₃ , we get
A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) = I ₃ .

Question 3.
Check whether the following matrices are invertible or not:
(i) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1 – 0 = 1 ≠ 0.
∴ A is a non-singular matrix.
Hence, A ^-1 exists.

(ii) \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right|\) = 1 – 1 = 0.
∴ A is a singular matrix.
Hence, A ^-1 does not exist.

(iii) \(\left[\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right|\) = 3 – 6 = -3 ≠ 0.
∴ A is a non-singular matrix.
Hence, A ^-1 exist.

(iv) \(\left[\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right|\) = 30 – 30 = 0.
∴ A is a singular matrix.
Hence, A ^-1 does not exist.

(v) \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{cc}
\sec \theta & \tan \theta \\
\tan \theta & \sec \theta
\end{array}\right|\)
= sec ² θ – tan ² θ = 1 ≠ 0.
∴ A is a non-singular matrix.
Hence, A ^-1 exist.

(vii) \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Solution:
let A = \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right|\)
= 3(5 – 0) – 4(5 – 0) + 3(4 – 1)
= 15 – 20 + 9 = 4 ≠ 0
∴ A is a non-singular matrix.
Hence, A ^-1 exist.

(viii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right|\)
= 1 (-3 -6) – 2 (6 – 3) + 3 (4 + 1)
= -9 – 6 + 15 = 0
∴ A is a singular matrix.
Hence, A ^-1 does not exist.

(ix) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right|\)
= 1(32 – 30) – 2(24 – 20) + 3(18 – 16)
= 2 – 8 + 6 = 0
∴ A is a singular matrix.
Hence, A ^-1 does not exist.

Question 4.
Find AB, if A = \(\left[\begin{array}{ccc}
1 & 2 & 3 \\
1 & -2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & -1 \\
1 & 2 \\
1 & -2
\end{array}\right]\) Examine whether AB has inverse or not.
Solution:

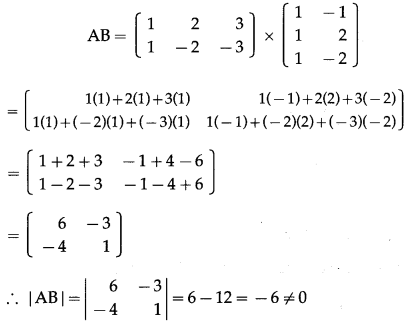
∴ A is a non-singular matrix.
Hence, (AB) ^-1 exist.

Question 5.
If A = \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\) is a nonsingular matrix then find A ^-1 by elementary row transformations.
Hence, find the inverse of \(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\)
Solution:
Since A is a non-singular matrix, then find A ^-1 by using elementary row transformations.
We write AA ^-1 = I

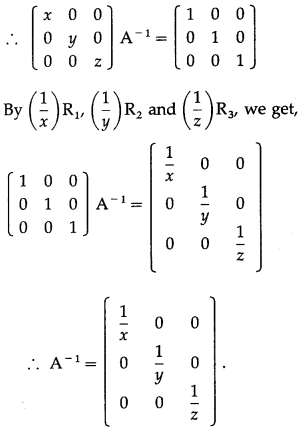
Comparing \(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) with \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\),
we get, x = 2, y = 1, z = -1
∴ \(\frac{1}{x}\) = \(\frac{1}{2}\), \(\frac{1}{y}\) = \(\frac{1}{1}\) = 1, \(\frac{1}{z}\) = \(\frac{1}{-1}\) = -1
\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) is \(\left(\begin{array}{rrr}
\frac{1}{2} & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right)\).

Question 6.
if A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\) and X is a 2 × 2 matrix such that AX = I , then find X.
Solution:
We will reduce the matrix A to the identity matrix by using row transformations. During this pro¬cess, I will be converted to the matrix X.
We have AX = I.

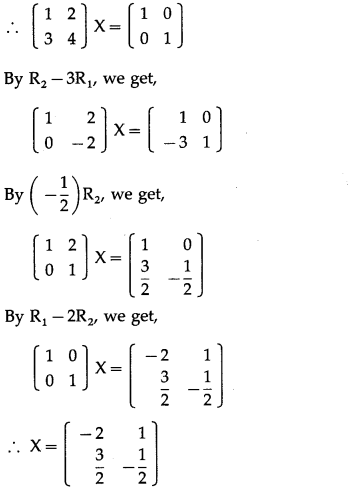
Question 7.
Find the inverse of each of the following matrices (if they exist).
(i) \(\left[\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right|\) = 3 + 2 = 5 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

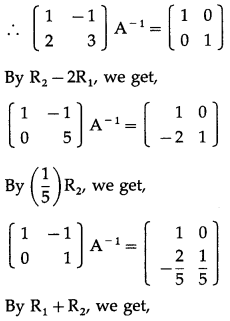
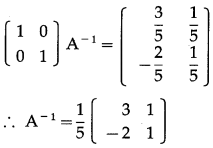
(ii) \(\left[\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right|\) = -2 – 1 = -3 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

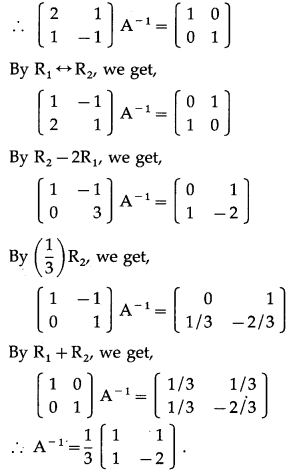
(iii) \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right|\) = 7 – 6 = 1 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

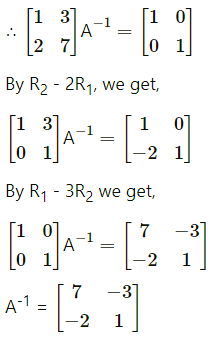
(iv) \(\left[\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right|\) = 14 + 15 = 29 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

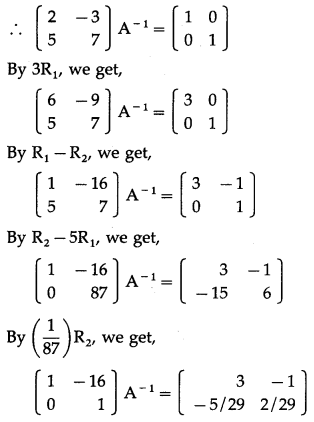
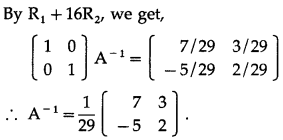
(v) \(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right|\) = 8 – 7 = 1 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

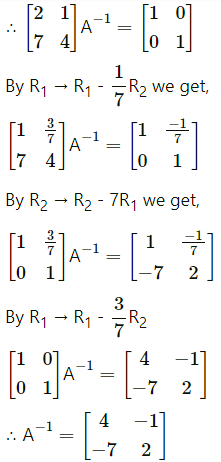
(vi) \(\left[\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right|\) = -21 + 20 = -1 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

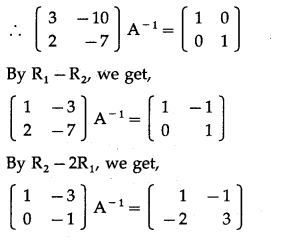
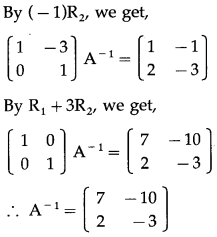
(vii) \(\left[\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right|\)
= 2(4 + 6) +3(4 – 9) + 3(-4 – 6)
= 20 – 15 – 30 = -25 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

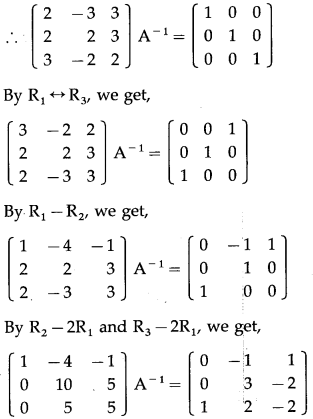
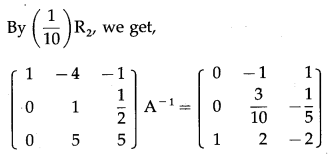
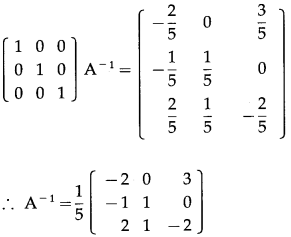
(viii) \(\left[\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right|\)
= 1(0 + 25) + 3(0 + 10) + 2(-15 – 0)
= 25 + 30 -30
= 25 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

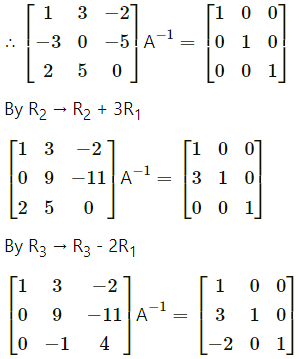
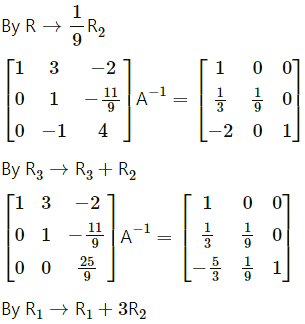
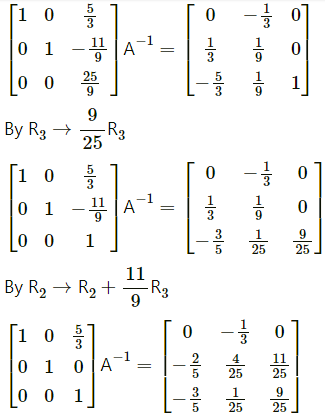
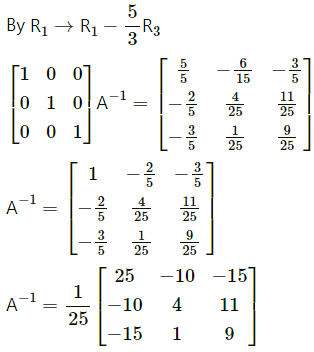
(ix) \(\left[\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:
Let A =\(\left[\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right|\)
= 2(3 – 0) – 0 – 1(5 – 0)
= 6 – 0 – 5 = 1 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I


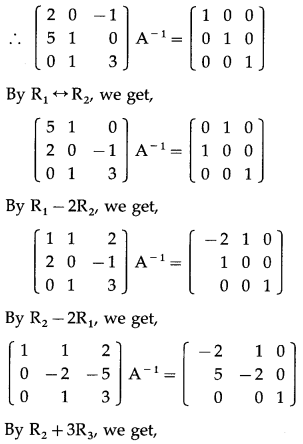
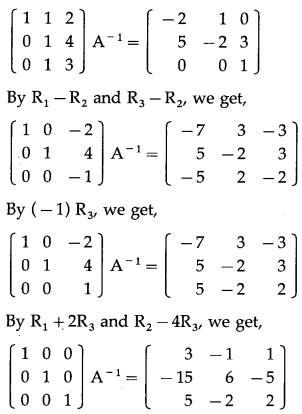
∴ A ^-1 = \(\left[\begin{array}{lll}
3 & -1 & 1 \\
-15 & 6 & -5 \\
5 & -2 & 2
\end{array}\right]\)

(x) \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
∴ A ^-1 = \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
= 1\(\left|\begin{array}{ll}
-2 & 1 \\
3 & 0
\end{array}\right|\) – 2\(\left|\begin{array}{ll}
0 & 1 \\
-1 & 1
\end{array}\right|\) – 2\(\left|\begin{array}{ll}
0 & -2 \\
-1 & 3
\end{array}\right|\)
|A| = 1(0 – 3) – 2(0 + 1) – 2(0 – 2)
= -3 – 2 + 4
= -1 ≠ 0
∴ A ^-1 exists.
We have
AA ^-1 = I


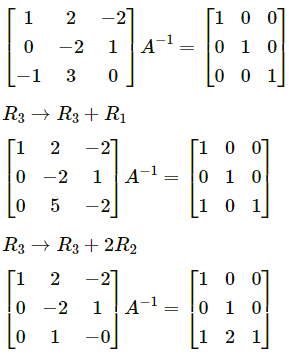
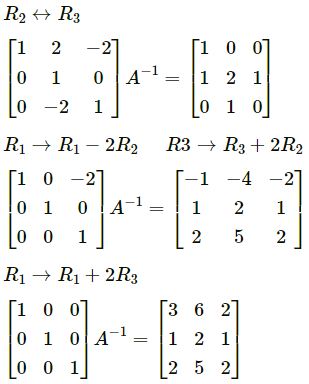
∴ A ^-1 = \(\left[\begin{array}{lll}
3 & 6 & 2 \\
1 & 2 & 1 \\
2 & 5 & 2
\end{array}\right]\)

Question 8.
Find the inverse of A = \(\left[\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right]\) by
(i) elementary row transformations
Solution:
|A| = \(\left|\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right|\)
= cosθ (cosθ – 0) + sinθ (sinθ – 0) + 0
= cos ² θ + sin ² θ = 1 ≠ 0
∴ A ^-1 exists.
(i) Consider AA ^-1 = I

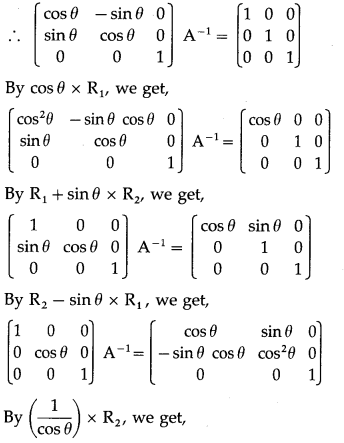
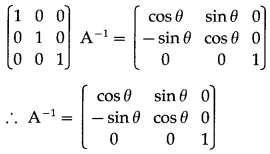
(ii) elementary column transformations
Solution:
Consider A ^-1 A = I

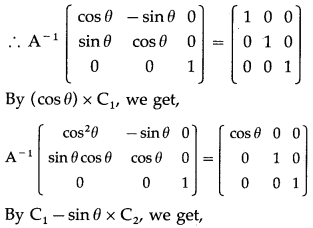
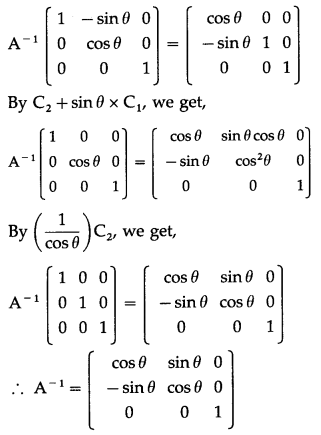
Question 9.
If A = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & 0 \\
3 & 1
\end{array}\right]\) find AB and (AB) ^-1 . Verify that (AB) ^-1 = B ^-1 A ^-1
Solution:
AB = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\) \(\left[\begin{array}{ll}
1 & 0 \\
3 & 1
\end{array}\right]\)




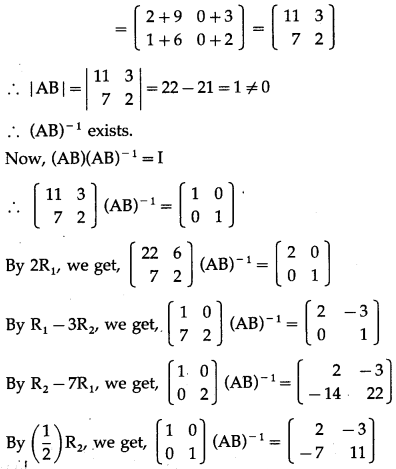
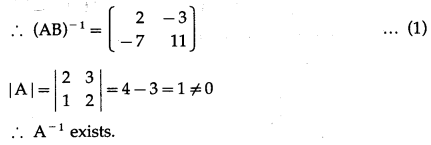
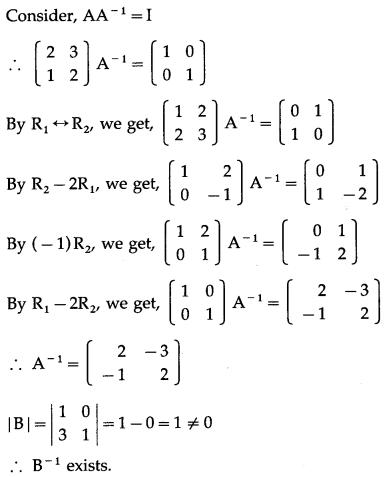
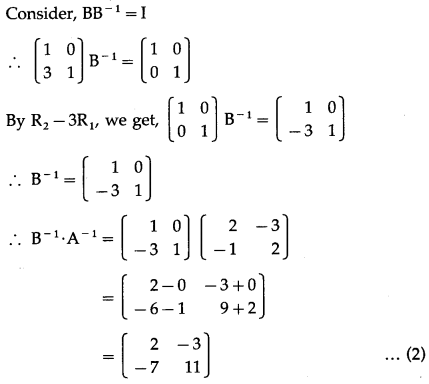
From (1) and (2), (AB) ^-1 = B ^-1 ∙ A ^-1 .

Question 10.
If A = \(\left[\begin{array}{ll}
4 & 5 \\
2 & 1
\end{array}\right]\), then show that A ^-1 = \(\frac{1}{6}\)(A – 5I)
Solution:
|A| = \(\left|\begin{array}{ll}
4 & 5 \\
2 & 1
\end{array}\right|\) = 4 – 10 = -6 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

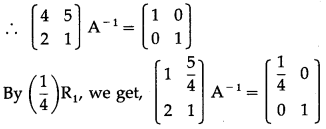
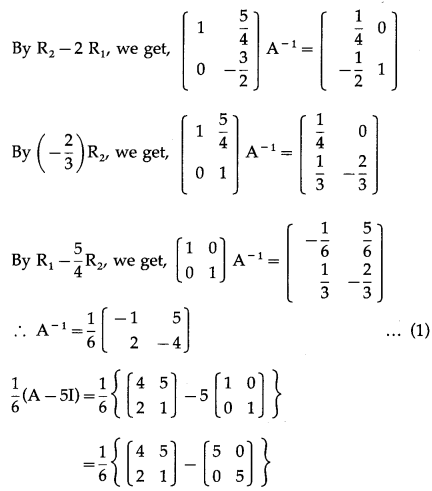
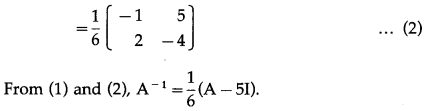
Question 11.
Find matrix X such that AX = B, where A = \(\left[\begin{array}{ll}
1 & 2 \\
-1 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
0 & 1 \\
2 & 4
\end{array}\right]\)
Solution:
AX = B

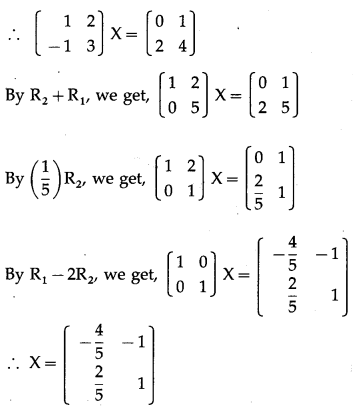
Question 12.
Find X, if AX = B where A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\).
Solution:
AX = B

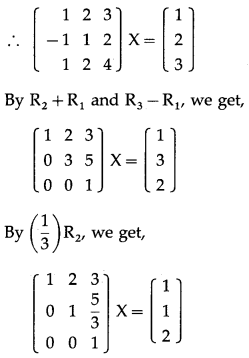
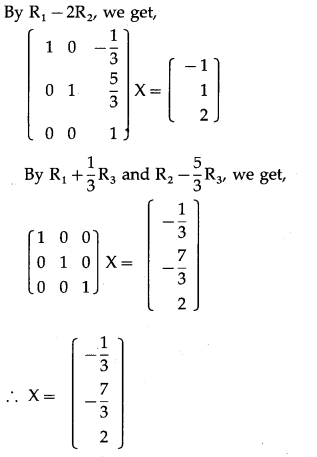
Question 13.
If A = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{ll}
4 & 1 \\
3 & 1
\end{array}\right]\) and C = \(\left[\begin{array}{ll}
24 & 7 \\
31 & 9
\end{array}\right]\) then find matrix X such that AXB = C.
Solution:
AXB = C
∴ \(\left(\begin{array}{ll}
1 & 1 \\
1 & 2
\end{array}\right)(\mathrm{XB})\) =\(\left[\begin{array}{ll}
24 & 7 \\
31 & 9
\end{array}\right]\)
First we perform the row transformations.

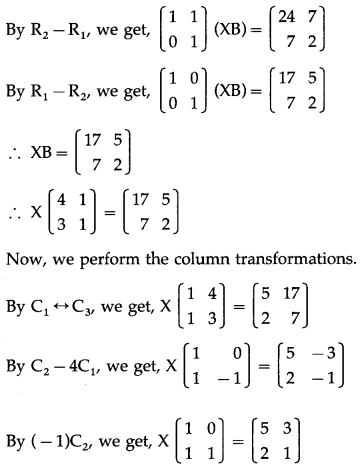
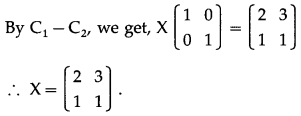
Question 14.
Find the inverse of \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\) by adjoint method.
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right|\)
= 1(7 – 20) – 2(7 – 10) + 3(4 – 2)
= -13 + 6 + 6 = -1 ≠ 0
∴ A ^-1 exists.
First we have to find the cofactor matrix
= [A _ij ] _3×3 where A _ij = (-1) ^i+j M _ij
Now, A ₁₁ = (-1) ¹⁺¹ M ₁₁ = \(\left|\begin{array}{ll}
1 & 5 \\
4 & 7
\end{array}\right|\) = 7 – 20 = -13
A ₁₂ = (-1) ¹⁺² M ₁₂ = \(\left|\begin{array}{ll}
1 & 5 \\
2 & 7
\end{array}\right|\) = -(7 – 10) = 3

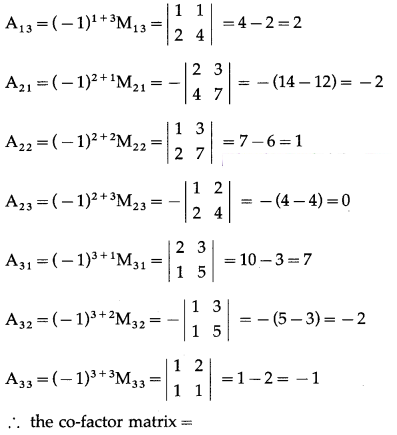
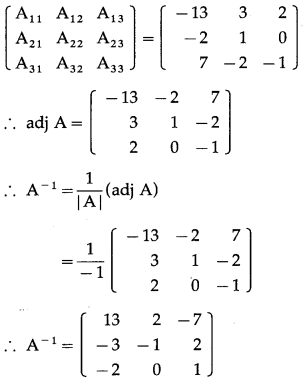
Question 15.
Find the inverse of \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) by adjoint method.
Solution:
where A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\)
|A| = 1(2 – 6) – 0(0 – 3) + 1(0 – 2)
|A| = -4 – 2
|A| = -6 ≠ 0
∴ A ^-1 exists.
First we have to find the cofactor matrix
= [A _ij ]3×3, where A _ij = (-1) ^i+j M _ij

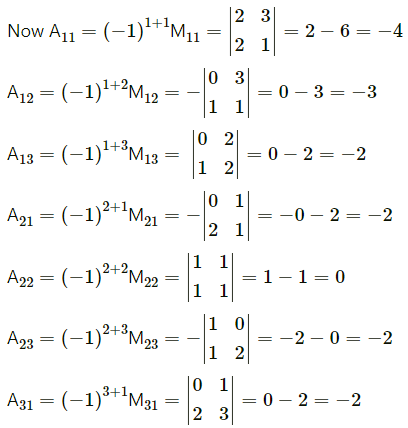
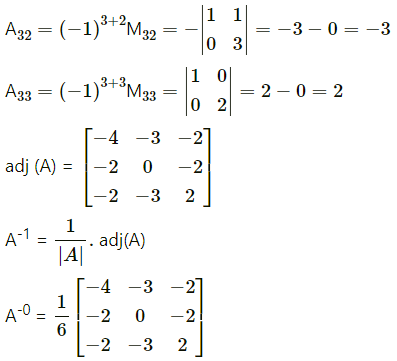
Question 16.
Find A ^-1 by adjoint method and by elementary transformations if A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right]\)
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right|\)
= 1(4 – 4) – 2(-4 – 2) + 3(-2 – 1)
= 0 + 12 – 9 = 3 ≠ 0
∴ A ^-1 exists.
A ^-1 by adjoint method :
We have to find the cofactor matrix
= [A _ij ] _3×3 , where A _ij = (-1) ^i+j M _ij

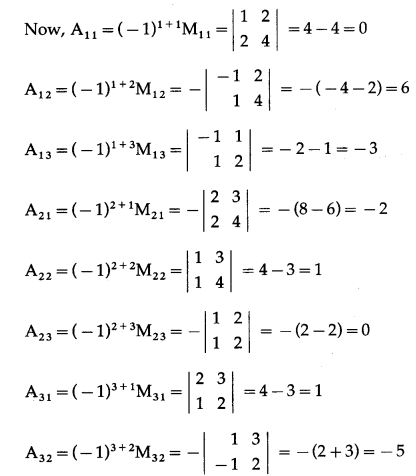
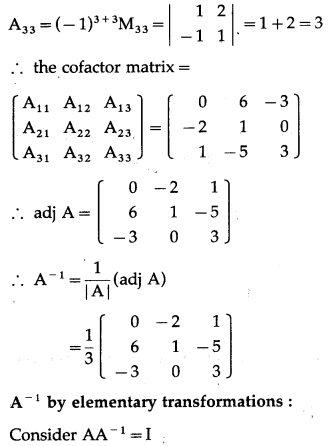
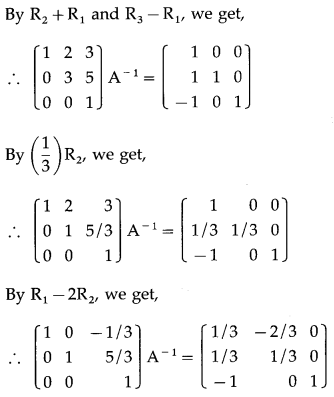
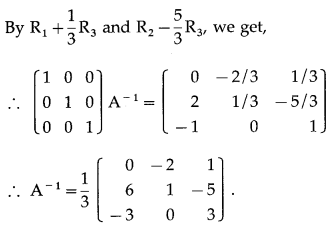
Question 17.
Find the inverse of A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) by elementary column transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right|\)
= 1 (2 – 6) – 0 + 1 (0 – 2)
= -4 – 2= -6 ≠ 0
∴ A ^-1 exists.
Consider A ^-1 A = I
∴ A ^-1 \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
By C ₃ – C ₁ , we get,

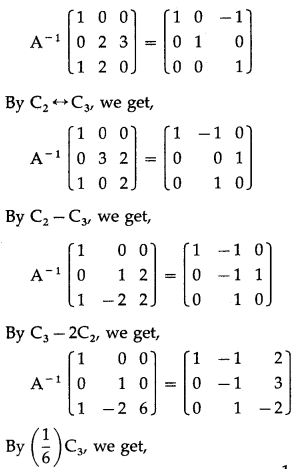
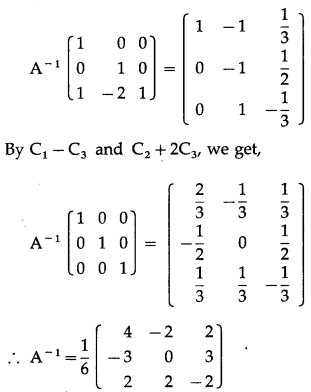
Question 18.
Find the inverse of \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\) by elementary row transformations.
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right|\)
= 1(7 – 20) – 2(7 – 10) + 3(4 – 2)
= -13 + 6 + 6 = -1 ≠ 0
∴ A ^-1 exists.
Consider AA ^-1 = I

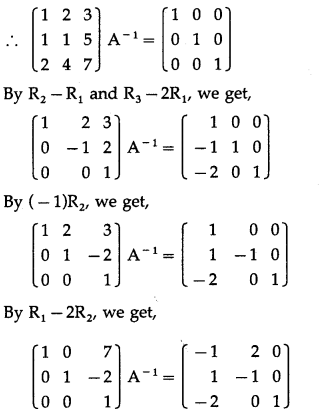
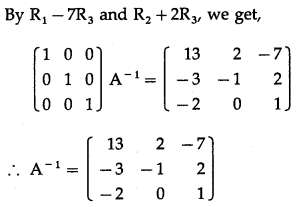
Question 19.
Show with usual notations that for any matrix A = [a _ij ] _3×3
(i) a ₁₁ A ₂₁ + a ₁₂ A ₂₂ + a ₁₃ A ₂₃ = 0
Solution:
A = [a _ij ] _3×3 = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\)
(i) A ₂₁ = (-1) ²⁺¹ M ₂₁ = \(-\left|\begin{array}{ll}
a_{12} & a_{13} \\
a_{32} & a_{33}
\end{array}\right|\)
= -(a ₁₂ a ₃₃ – a ₁₃ a ₃₂ )
= -a ₁₂ a ₃₃ + a ₁₃ a ₃₂
A ₂₂ = (-1) ²⁺² M ₂₂ = \(\left|\begin{array}{ll}
a_{11} & a_{13} \\
a_{31} & a_{33}
\end{array}\right|\)
= a ₁₁ a ₃₃ – a ₁₃ a ₃₁
A ₂₃ = (-1) ²⁺³ M ₂₃ = \(-\left|\begin{array}{ll}
a_{11} & a_{12} \\
a_{31} & a_{32}
\end{array}\right|\)
= -(a ₁₁ a ₃₂ – a ₁₂ a ₃₁ )
= -a ₁₁ a ₃₂ + a ₁₂ a ₃₁
∴ a ₁₁ A ₂₁ + a ₁₂ A ₂₂ + a ₁₃ A ₂₃
= a ₁₁ (-a _{12 33} + a ₁₃ a ₃₂ ) + a ₁₂ (a ₁₁ a ₃₃ – a ₁₃ a ₃₁ ) + a ₁₃ (-a ₁₁ a ₃₂ + a ₁₂ a ₃₁ )
= -a ₁₁ a ₁₂ a ₃₃ + a ₁₁ a ₁₃ a ₃₂ + a ₁₁ a ₁₂ a ₃₃ – a ₁₂ a ₁₃ a ₃₁ – a ₁₁ a ₁₃ a ₃₂ + a ₁₂ a ₁₃ a ₃₁
= 0

(ii) a ₁₁ A ₁₁ + a ₁₂ A ₁₂ + a ₁₃ A ₁₃ = |A|
Solution:

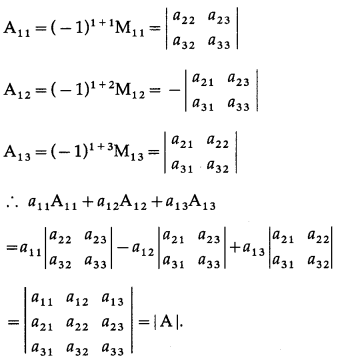
Question 20.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\), then find a matrix X such that XA= B.
Solution:
Consider XA = B