Differential Equations Class 12 Maths 2 Exercise 6.3 Solutions Maharashtra Board

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.3 Questions and Answers.

12th Maths Part 2 Differential Equations Exercise 6.3 Questions And Answers Maharashtra Board

Question 1.
In each of the following examples verify that the given expression is a solution of the corresponding differential equation.
(i) xy = log y + c; $\frac{d y}{d x}=\frac{y^{2}}{1-x y}$
Solution:
xy = log y + c
Differentiating w.r.t. x, we get

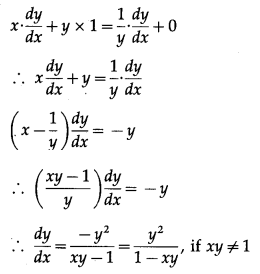
Hence, xy = log y + c is a solution of the D.E.
$\frac{d y}{d x}=\frac{y^{2}}{1-x y^{\prime}}, x y \neq 1$

(ii) y = (sin ^-1 x) ² + c; (1 – x ² ) $\frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}=2$
Solution:
y = (sin ^-1 x) ² + c …….(1)
Differentiating w.r.t. x, we get

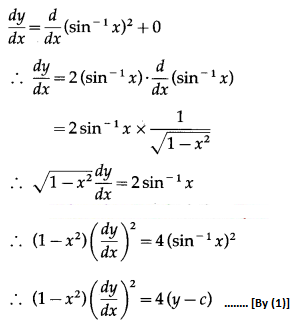
Differentiating again w.r.t. x, we get

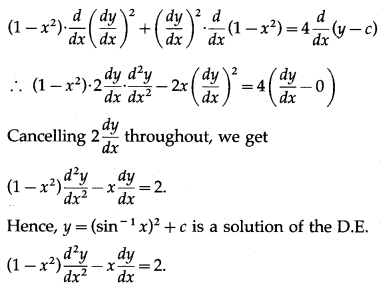
(iii) y = e ^-x + Ax + B; $e^{x} \frac{d^{2} y}{d x^{2}}=1$
Solution:
y = e ^-x + Ax + B
Differentiating w.r.t. x, we get

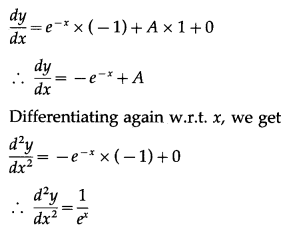
∴ $e^{x} \frac{d^{2} y}{d x^{2}}=1$
Hence, y = e ^-x + Ax + B is a solution of the D.E.
$e^{x} \frac{d^{2} y}{d x^{2}}=1$

(iv) y = x ^m ; $x^{2} \frac{d^{2} y}{d x^{2}}-m x \frac{d y}{d x}+m y=0$
Solution:
y = x ^m
Differentiating twice w.r.t. x, we get

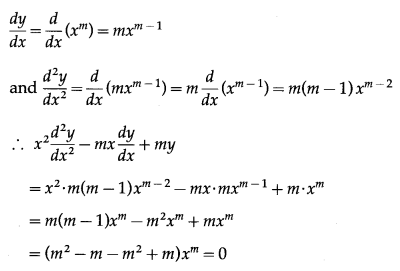
This shows that y = x ^m is a solution of the D.E.
$x^{2} \frac{d^{2} y}{d x^{2}}-m x \frac{d y}{d x}+m y=0$

(v) y = a + $\frac{b}{x}$; $x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0$
Solution:
y = a + $\frac{b}{x}$
Differentiating w.r.t. x, we get

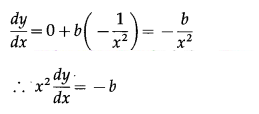
Differentiating again w.r.t. x, we get

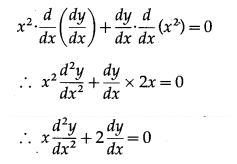
Hence, y = a + $\frac{b}{x}$ is a solution of the D.E.
$x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0$

(vi) y = e ^ax ; x $\frac{d y}{d x}$ = y log y
Solution:
y = e ^ax
log y = log e ^ax = ax log e
log y = ax …….(1) ……..[∵ log e = 1]
Differentiating w.r.t. x, we get
$\frac{1}{y} \cdot \frac{d y}{d x}$ = a × 1
∴ $\frac{d y}{d x}$ = ay
∴ x $\frac{d y}{d x}$ = (ax)y
∴ x $\frac{d y}{d x}$ = y log y ………[By (1)]
Hence, y = e ^ax is a solution of the D.E.
x $\frac{d y}{d x}$ = y log y.

Question 2.
Solve the following differential equations.
(i) $\frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}}$
Solution:

(ii) log($\frac{d y}{d x}$) = 2x + 3y
Solution:

(iii) y – x $\frac{d y}{d x}$ = 0
Solution:
y – x $\frac{d y}{d x}$ = 0
∴ x $\frac{d y}{d x}$ = y
∴ $\frac{1}{x} d x=\frac{1}{y} d y$
Integrating both sides, we get
$\int \frac{1}{x} d x=\int \frac{1}{y} d y$
∴ log |x| = log |y| + log c
∴ log |x| = log |cy|
∴ x = cy
This is the general solution.

(iv) sec ² x . tan y dx + sec ² y . tan x dy = 0
Solution:
sec ² x . tan y dx + sec ² y . tan x dy = 0
∴ $\frac{\sec ^{2} x}{\tan x} d x+\frac{\sec ^{2} y}{\tan y} d y=0$
Integrating both sides, we get
$\int \frac{\sec ^{2} x}{\tan x} d x+\int \frac{\sec ^{2} y}{\tan y} d y=c_{1}$
Each of these integrals is of the type
$\int \frac{f^{\prime}(x)}{f(x)} d x$ = log |f(x)| + c
∴ the general solution is
∴ log|tan x| + log|tan y | = log c, where c ₁ = log c
∴ log |tan x . tan y| = log c
∴ tan x . tan y = c
This is the general solution.

(v) cos x . cos y dy – sin x . sin y dx = 0
Solution:
cos x . cos y dy – sin x . sin y dx = 0
$\frac{\cos y}{\sin y} d y-\frac{\sin x}{\cos x} d x=0$
Integrating both sides, we get
∫cot y dy – ∫tan x dx = c ₁
∴ log|sin y| – [-log|cos x|] = log c, where c ₁ = log c
∴ log |sin y| + log|cos x| = log c
∴ log|sin y . cos x| = log c
∴ sin y . cos x = c
This is the general solution.

(vi) $\frac{d y}{d x}$ = -k, where k is a constant.
Solution:
$\frac{d y}{d x}$ = -k
∴ dy = -k dx
Integrating both sides, we get
∫dy = -k∫dx
∴ y = -kx + c
This is the general solution.

(vii) $\frac{\cos ^{2} y}{x} d y+\frac{\cos ^{2} x}{y} d x=0$
Solution:
$\frac{\cos ^{2} y}{x} d y+\frac{\cos ^{2} x}{y} d x=0$
∴ y cos ² y dy + x cos ² x dx = 0
∴ $x\left(\frac{1+\cos 2 x}{2}\right) d x+y\left(1+\frac{\cos 2 y}{2}\right) d y=0$
∴ x(1 + cos 2x) dx + y(1 + cos 2y) dy = 0
∴ x dx + x cos 2x dx + y dy+ y cos 2y dy = 0
Integrating both sides, we get
∫x dx + ∫y dy + ∫x cos 2x dx + ∫y cos 2y dy = c ₁ ……..(1)
Using integration by parts

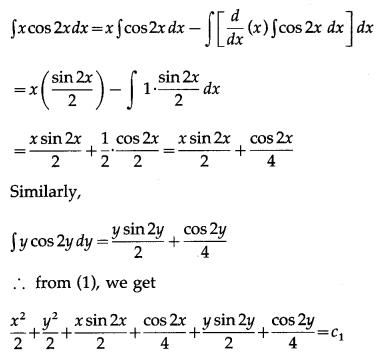
Multiplying throughout by 4, this becomes
2x ² + 2y ² + 2x sin 2x + cos 2x + 2y sin 2y + cos 2y = 4c ₁
∴ 2(x ² + y ² ) + 2(x sin 2x + y sin 2y) + cos 2y + cos 2x + c = 0, where c = -4c ₁
This is the general solution.

(viii) $y^{3}-\frac{d y}{d x}=x^{2} \frac{d y}{d x}$
Solution:

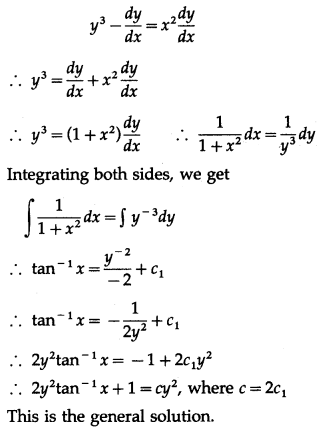
(ix) 2e ^x+2y dx – 3 dy = 0
Solution:

(x) $\frac{d y}{d x}$ = e ^x+y + x ² e ^y
Solution:

∴ 3e ^x + 3e ^-y + x ³ = -3c ₁
∴ 3e ^x + 3e ^-y + x ³ = c, where c = -3c ₁
This is the general solution.

Question 3.
For each of the following differential equations, find the particular solution satisfying the given condition:
(i) 3e ^x tan y dx + (1 + e ^x ) sec ² y dy = 0, when x = 0, y = π
Solution:
3e ^x tan y dx + (1 + e ^x ) sec ² y dy = 0

(ii) (x – y ² x) dx – (y + x ² y) dy = 0, when x = 2, y = 0
Solution:
(x – y ² x) dx – (y + x ² y) dy = 0
∴ x(1 – y ² ) dx – y(1 + x ² ) dy = 0

When x = 2, y = 0, we have
(1 + 4)(1 – 0) = c
∴ c = 5
∴ the particular solution is (1 + x ² )(1 – y ² ) = 5.

(iii) y(1 + log x) $\frac{d x}{d y}$ – x log x = 0, y = e ² , when x = e
Solution:
y(1 + log x) $\frac{d x}{d y}$ – x log x = 0

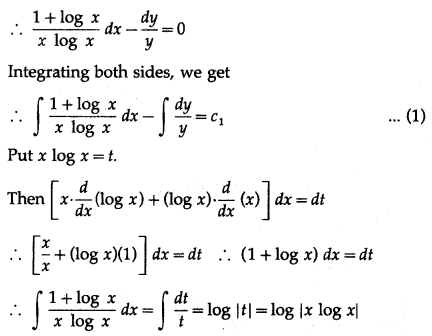
(iv) (e ^y + 1) cos x + e ^y sin x $\frac{d y}{d x}$ = 0, when x = $\frac{\pi}{6}$, y = 0
Solution:
(e ^y + 1) cos x + e ^y sin x $\frac{d y}{d x}$ = 0

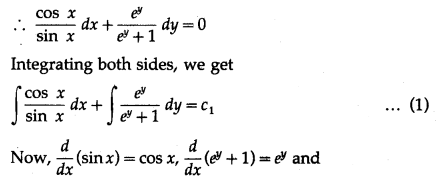
$\int \frac{f^{\prime}(x)}{f(x)} d x$ = log|f(x)| + c
∴ from (1), the general solution is
log|sin x| + log|e ^y + 1| = log c, where c ₁ = log c
∴ log|sin x . (e ^y + 1)| = log c
∴ sin x . (e ^y + 1) = c
When x = $\frac{\pi}{4}$, y = 0, we get
$\left(\sin \frac{\pi}{4}\right)\left(e^{0}+1\right)=c$
∴ c = $\frac{1}{\sqrt{2}}$(1 + 1) = √2
∴ the particular solution is sin x . (e ^y + 1) = √2

(v) (x + 1) $\frac{d y}{d x}$ – 1 = 2e ^-y , y = 0, when x = 1
Solution:

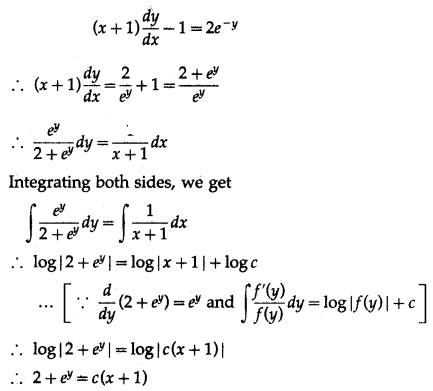
This is the general solution.
Now, y = 0, when x = 1
∴ 2 + e ⁰ = c(1 + 1)
∴ 3 = 2c
∴ c = $\frac{3}{2}$
∴ the particular solution is 2 + e ^y = $\frac{3}{2}$ (x + 1)
∴ 2(2 + e ^y ) = 3(x + 1).

(vi) cos($\frac{d y}{d x}$) = a, a ∈ R, y (0) = 2
Solution:
cos($\frac{d y}{d x}$) = a
∴ $\frac{d y}{d x}$ = cos ^-1 a
∴ dy = (cos ^-1 a) dx
Integrating both sides, we get
∫dy = (cos ^-1 a) ∫dx
∴ y = (cos ^-1 a) x + c
∴ y = x cos ^-1 a + c
This is the general solution.
Now, y(0) = 2, i.e. y = 2,
when x = 0, 2 = 0 + c
∴ c = 2
∴ the particular solution is
∴ y = x cos ^-1 a + 2
∴ y – 2 = x cos ^-1 a
∴ $\frac{y-2}{x}$ = cos ^-1 a
∴ cos($\frac{y-2}{x}$) = a

Question 4.
Reduce each of the following differential equations to the variable separable form and hence solve:
(i) $\frac{d y}{d x}$ = cos(x + y)
Solution:

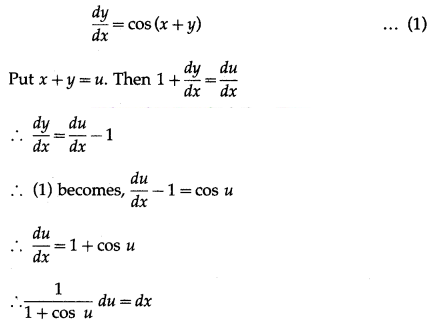
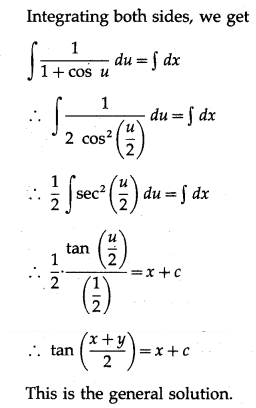
(ii) (x – y) ² $\frac{d y}{d x}$ = a ²
Solution:

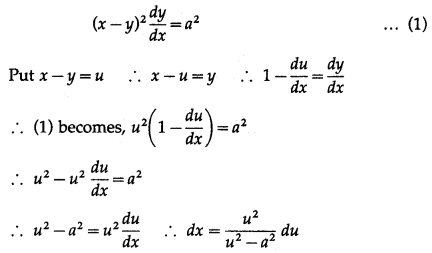
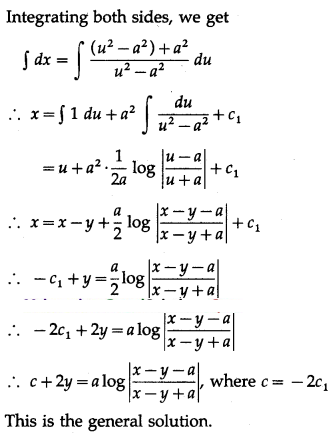
(iii) x + y $\frac{d y}{d x}$ = sec(x ² + y ² )
Solution:

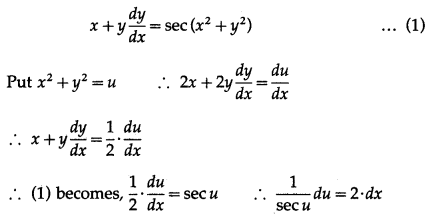
Integrating both sides, we get
∫cos u du = 2 ∫dx
∴ sin u = 2x + c
∴ sin(x ² + y ² ) = 2x + c
This is the general solution.

(iv) cos ² (x – 2y) = 1 – 2 $\frac{d y}{d x}$
Solution:

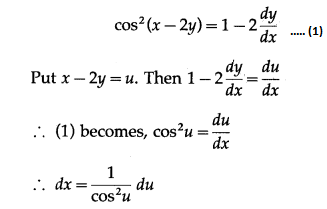
Integrating both sides, we get
∫dx = ∫sec ² u du
∴ x = tan u + c
∴ x = tan(x – 2y) + c
This is the general solution.

(v) (2x – 2y + 3) dx – (x – y + 1) dy = 0, when x = 0, y = 1
Solution:
(2x – 2y + 3) dx – (x – y + 1) dy = 0
∴ (x – y + 1) dy = (2x – 2y + 3) dx
∴ $\frac{d y}{d x}=\frac{2(x-y)+3}{(x-y)+1}$ ………(1)
Put x – y = u, Then $1-\frac{d y}{d x}=\frac{d u}{d x}$

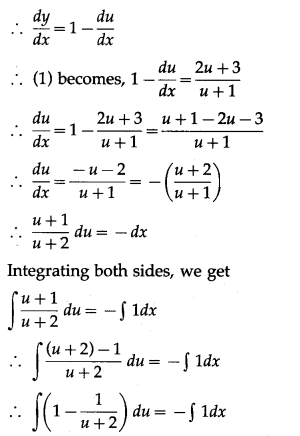
∴ u – log|u + 2| = -x + c
∴ x – y – log|x – y + 2| = -x + c
∴ (2x – y) – log|x – y + 2| = c
This is the general solution.
Now, y = 1, when x = 0.
∴ (0 – 1) – log|0 – 1 + 2| = c
∴ -1 – o = c
∴ c = -1
∴ the particular solution is
(2x – y) – log|x – y + 2| = -1
∴ (2x – y) – log|x – y + 2| + 1 = 0