Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Linear Programming Ex 7.4 Questions and Answers.
12th Maths Part 1 Linear Programming Exercise 7.4 Questions And Answers Maharashtra Board
Question 1.
Maximize : z = 11x + 8y subject to x ≤ 4, y ≤ 6,
x + y ≤ 6, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and ED whose equations are x = 4, y = 6 and x + y = 6 respectively.
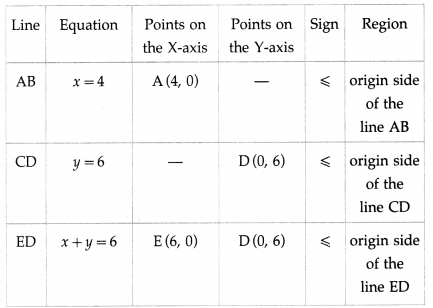
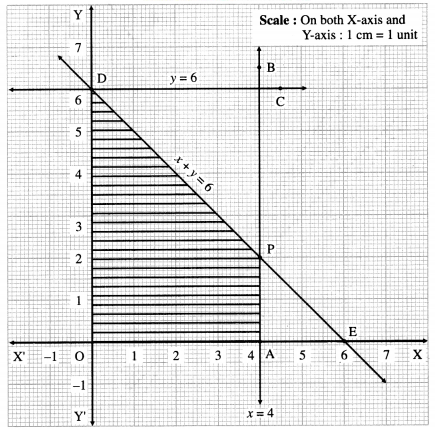
The feasible region is shaded portion OAPDO in the graph.
The vertices of the feasible region are O (0, 0), A (4, 0), P and D (0, 6)
P is point of intersection of lines x + y = 6 and x = 4.
Substituting x = 4 in x + y = 6, we get
4 + y = 6 ∴ y = 2 ∴ P is (4, 2).
∴ the corner points of feasible region are O (0, 0), A (4, 0), P(4, 2) and D(0 ,6).
The values of the objective function z = 11x + 8y at these vertices are
z (O) = 11(0) + 8(0) = 0 + 0 = 0
z(a) = 11(4) + 8(0) = 44 + 0 = 44
z (P) = 11(4) + 8(2) = 44 + 16 = 60
z (D) = 11(0) + 8(2) = 0 + 16 = 16
∴ z has maximum value 60, when x = 4 and y = 2.
Question 2.
Maximize : z = 4x + 6y subject to 3x + 2y ≤ 12,
x + y ≥ 4, x, y ≥ 0.
Solution:
First we draw the lines AB and AC whose equations are 3x + 2y = 12 and x + y = 4 respectively.
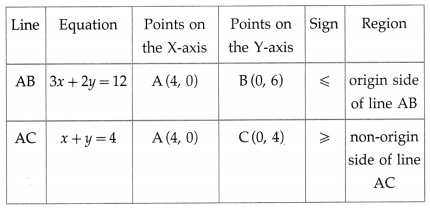
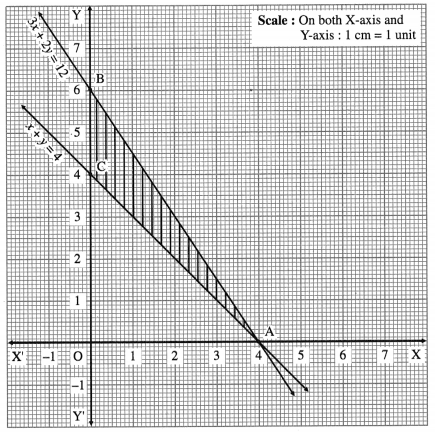
The feasible region is the ∆ABC which is shaded in the graph.
The vertices of the feasible region (i.e. corner points) are A (4, 0), B (0, 6) and C (0, 4).
The values of the objective function z = 4x + 6y at these vertices are
z(a) = 4(4) + 6(0) = 16 + 0 = 16
z(B) = 4(0)+ 6(6) = 0 + 36 = 36
z(C) = 4(0) + 6(4) = 0 + 24 = 24
∴ has maximum value 36, when x = 0, y = 6.

Question 3.
Maximize : z = 7x + 11y subject to 3x + 5y ≤ 26
5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB and CD whose equations are 3x + 5y = 26 and 5x + 3y = 30 respectively.
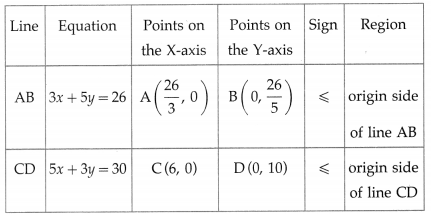
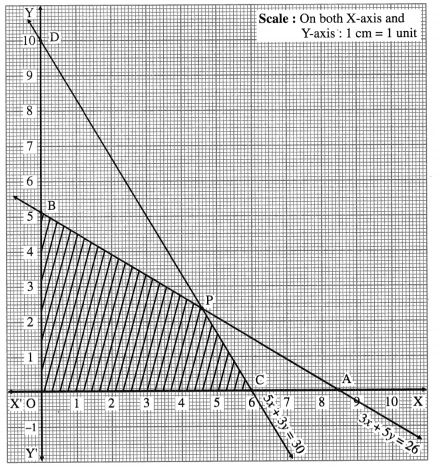
The feasible region is OCPBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (6, 0), p and B(0, \(\frac{26}{5}\))
The vertex P is the point of intersection of the lines
3x + 5y = 26 … (1)
and 5x + 3y = 30 … (2)
Multiplying equation (1) by 3 and equation (2) by 5, we get
9x + 15y = 78
and 25x + 15y = 150
On subtracting, we get
16x = 72 ∴ x = \(\frac{72}{16}=\frac{9}{2}\) = 4.5
Substituting x = 4.5 in equation (2), we get
5(4.5) + 3y = 30
22.5 + 3y = 30
∴ 3y = 7.5 ∴ y = 2.5
∴ P is (4.5, 2.5)
The values of the objective function z = 7x + 11y at these corner points are
z (O) = 7(0) + 11(0) = 0 + 0 = 0
z (C) = 7(6) + 11(0) = 42 + 0 = 42
z (P) = 7(4.5) + 11 (2.5) = 31.5 + 27.5 = 59.0 = 59
z(B) = 7(0) + 11\(\left(\frac{26}{5}\right)=\frac{286}{5}\) = 57.2
∴ z has maximum value 59, when x = 4.5 and y = 2.5.
Question 4.
Maximize : z = 10x + 25y subject to 0 ≤ x ≤ 3,
0 ≤ y ≤ 3, x + y ≤ 5 also find maximum value of z.
Solution:
First we draw the lines AB, CD and EF whose equations are x = 3, y = 3 and x + y = 5 respectively.
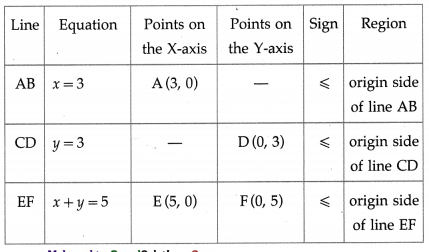
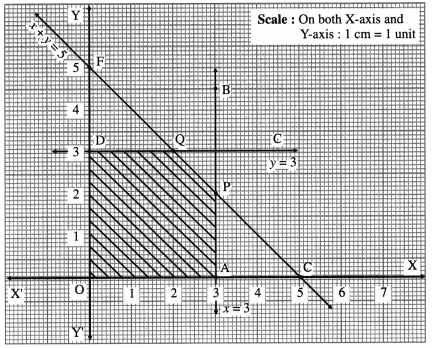
The feasible region is OAPQDO which is shaded in the i graph.
The vertices of the feasible region are O (0, 0), A (3, 0), P, Q and D(0, 3).
t P is the point of intersection of the lines x + y = 5 and x = 3.
Substituting x = 3 in x + y = 5, we get
3 + y = 5 ∴ y = 2
∴ P is (3, 2)
Q is the point of intersection of the lines x + y = 5 and y = 3
Substituting y = 3 in x + y = 5, we get
x + 3 = 5 ∴ x = 2
∴ Q is (2, 3)
The values of the objective function z = 10x + 25y at these vertices are
z(O) = 10(0) + 25(0) = 0 + 0 = 0
z(a) = 10(3) + 25(0) = 30 + 0 = 30
z(P) = 10(3) + 25(2) = 30 + 50 = 80
z(Q) = 10(2) + 25(3) = 20 + 75 = 95
z(D) = 10(0)+ 25(3) = 0 + 75 = 75
∴ z has maximum value 95, when x = 2 and y = 3.

Question 5.
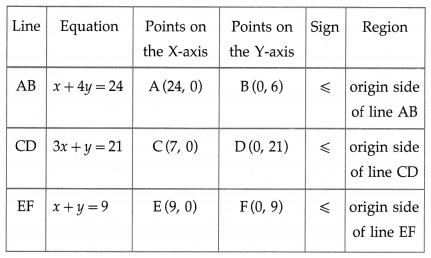
Maximize : z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21,
x + y ≤ 9, x ≥ 0, y ≥ 0 also find maximum value of z.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 4y = 24, 3x + y = 21 and x + y = 9 respectively.
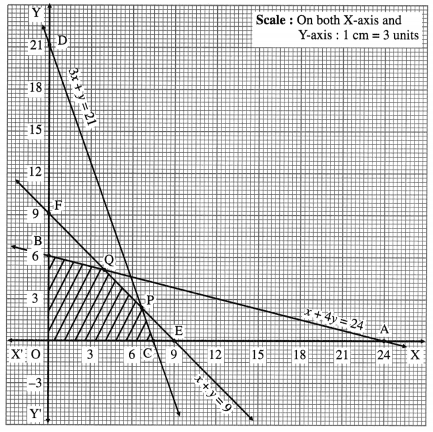
The feasible region is OCPQBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (7, 0), P, Q and B (0, 6).
P is the point of intersection of the lines
3x + y = 21 … (1)
and x + y = 9 … (2)
On subtracting, we get 2x = 12 ∴ x = 6
Substituting x = 6 in equation (2), we get
6 + y = 9 ∴ y = 3
∴ P = (6, 3)
Q is the point of intersection of the lines
x + 4y = 24 … (3)
and x + y = 9 … (2)
On subtracting, we get
3y = 15 ∴ y = 5
Substituting y = 5 in equation (2), we get
x + 5= 9 ∴ x = 4
∴ Q = (4, 5)
∴ the corner points of the feasible region are 0(0,0), C(7, 0), P (6, 3), Q (4, 5) and B (0, 6).
The values of the objective function 2 = 3x + 5y at these corner points are
z(O) = 3(0)+ 5(0) = 0 + 0 = 0
z(C) = 3(7) + 5(0) = 21 + 0 = 21
z(P) = 3(6) + 5(3) = 18 + 15 = 33
z(Q) = 3(4) + 5(5) = 12 + 25 = 37
z(B) = 3(0)+ 5(6) = 0 + 30 = 30
∴ z has maximum value 37, when x = 4 and y = 5.
Question 6.
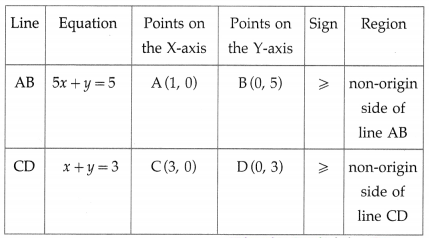
Minimize : z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3,
x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB and CD whose equations are 5x + y = 5 and x + y = 3 respectively.
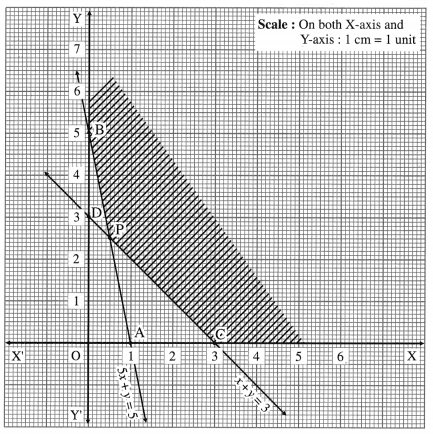
The feasible region is XCPBY which is shaded in the graph.
The vertices of the feasible region are C (3, 0), P and B (0, 5).
P is the point of the intersection of the lines
5x + y = 5
and x + y = 3
On subtracting, we get
4x = 2 ∴ x = \(\frac{1}{2}\)
Substituting x = \(\frac{1}{2}\) in x + y = 3, we get
\(\frac{1}{2}\) + y = 3
∴ y = \(\frac{5}{2}\) ∴ P = \(\left(\frac{1}{2}, \frac{5}{2}\right)\)
The values of the objective function z = 7x + y at these vertices are
z(C) = 7(3) + 0 = 21
z(B) = 7(0) + 5 = 5
∴ z has minimum value 5, when x = 0 and y = 5.

Question 7.
Minimize : z = 8x + 10y subject to 2x + y ≥ 7, 2x + 3y ≥ 15,
y ≥ 2, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are 2x + y = 7, 2x + 3y = 15 and y = 2 respectively.
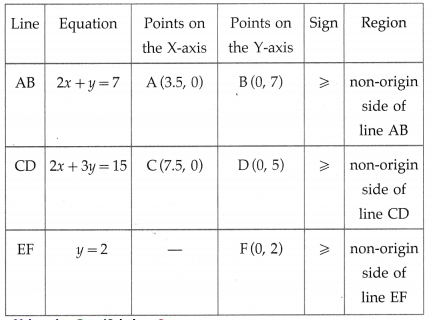
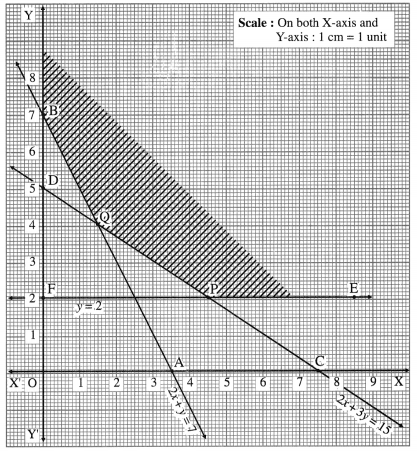
The feasible region is EPQBY which is shaded in the graph. The vertices of the feasible region are P, Q and B(0,7). P is the point of intersection of the lines 2x + 3y = 15 and y = 2.
Substituting y – 2 in 2x + 3y = 15, we get 2x + 3(2) = 15
∴ 2x = 9 ∴ x = 4.5 ∴ P = (4.5, 2)
Q is the point of intersection of the lines
2x + 3y = 15 … (1)
and 2x + y = 7 … (2)
On subtracting, we get
2y = 8 ∴ y = 4
∴ from (2), 2x + 4 = 7
∴ 2x = 3 ∴ x = 1.5
∴ Q = (1.5, 4)
The values of the objective function z = 8x + 10y at these vertices are
z(P) = 8(4.5) + 10(2) = 36 + 20 = 56
z(Q) = 8(1.5) + 10(4) = 12 + 40 = 52
z(B) = 8(0) +10(7) = 70
∴ z has minimum value 52, when x = 1.5 and y = 4
Question 8.
Minimize : z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4,
3x + y ≥ 3, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 2y = 3, x + 4y = 4 and 3x + y = 3 respectively.
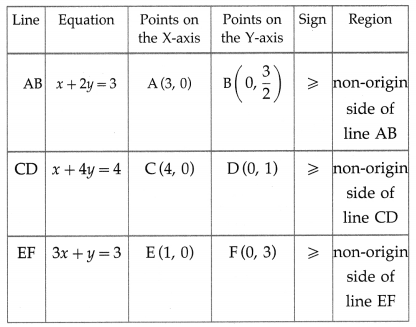
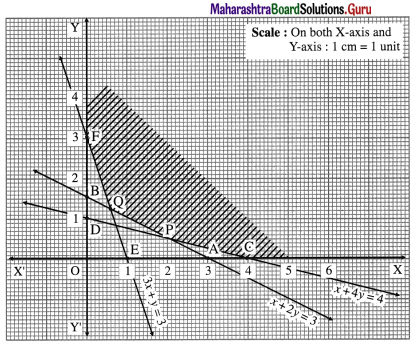
The feasible region is XCPQFY which is shaded in the graph.
The vertices of the feasible region are C (4, 0), P, Q and F(0, 3).
P is the point of intersection of the lines x + 4y = 4 and x + 2y = 3
On subtracting, we get
2y = 1 ∴ y = \(\frac{1}{2}\)
Substituting y = \(\frac{1}{2}\) in x + 2y = 3, we get
x + 2\(\left(\frac{1}{2}\right)\) = 3
∴ x = 2
∴ P = (2, \(\frac{1}{2}\))
Q is the point of intersection of the lines
x + 2y = 3 … (1)
and 3x + y = 3 ….(2)
Multiplying equation (1) by 3, we get 3x + 6y = 9
Subtracting equation (2) from this equation, we get
5y = 6
∴ y = \(\frac{6}{5}\)
∴ from (1), x + 2\(\left(\frac{6}{5}\right)\) = 3
∴ x = 3 – \(\frac{12}{5}=\frac{3}{5}\)
Q ≡ \(\left(\frac{3}{5}, \frac{6}{5}\right)\)
The values of the objective function z = 6x + 21y at these vertices are
z(C) = 6(4) + 21(0) = 24
z(P) = 6(2) + 21\(\left(\frac{1}{2}\right)\)
= 12 + 10.5 = 22.5
z(Q)= 6\(\left(\frac{3}{5}\right)\) + 21\(\left(\frac{6}{5}\right)\)
= \(\frac{18}{5}+\frac{126}{5}=\frac{144}{5}\) = 28.8
2 (F) = 6(0) + 21(3) = 63
∴ z has minimum value 22.5, when x = 2 and y = \(\frac{1}{2}\).