Fractions Class 5 Problem Set 17 Question Answer Maharashtra Board
Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 17 Textbook Exercise Important Questions and Answers.
Std 5 Maths Chapter 5 Fractions
Question 1.
Write the proper number in the box.
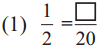
Answer:
Here 20 = 2 x 10
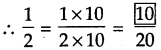
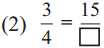
Answer:
Here 15 = 3 x 5
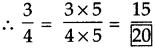
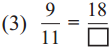
Answer:
Here 18 = 9 x 2
hehce,
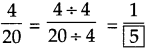
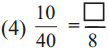
Answer:
Here 40 + 5 = 8,
hence,
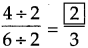
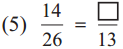
Answer:
Here 26 ÷ 2 = 13,
hence,
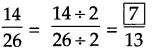
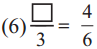
Answer:
Here 6 ÷ 2 = 3,
hence,
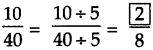
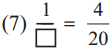
Answer:
Here 4 ÷ 4 = 1,
hence,
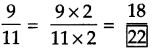
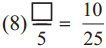
Answer:
Here 25 ÷ 5 = 5,
hence,
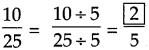
Question 2.
Find an equivalent fraction with denominator 18, for each of the following fractions.
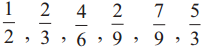
Solution:
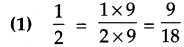
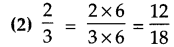
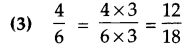
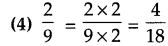
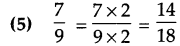
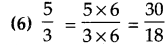
Question 3.
Find an equivalent fraction with denominator 5, for each of the following fractions.
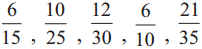
Solution:
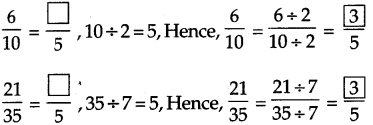
Question 4.
From the fractions given below, pair off the equivalent fractions.
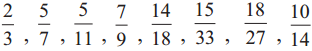
Solution:
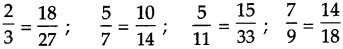
Question 5.
Find two equivalent fractions for each of the following fractions.
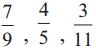
Solution:
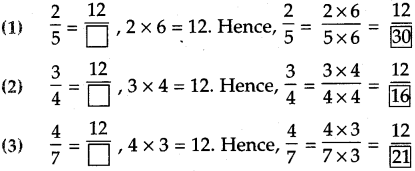
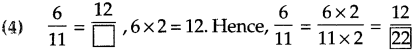
Like fractions and unlike fractions
Fractions such as \(\frac{1}{7}, \frac{4}{7}, \frac{6}{7}\) whose denominators are equal, are called ‘like fractions’.
Fractions such as \(\frac{1}{3}, \frac{4}{8}, \frac{9}{11}\) which have different denominators are called unlike fractions’.
Converting unlike fractions into like fractions
Example (1) Convert 5/6 and 7/9 into like fractions.
Here, we must find a common multiple for the numbers 6 and 9.
Multiples of 6 : 6, 12, 18, 24, 30, 36, ……..
Multiples of 9 : 9, 18, 27, 36, 45 ……..
Here, the number 18 is a multiple of both 6 and 9. So, let us make 18 the denominator of both fractions.
Thus, 15/18 and 1418 are like fractions, respectively equivalent to 5/6 and 7/9.
Here, 18 is a multiple of both 6 and 9. We could also choose numbers like 36 and 54 as the common denominators.
Example (2) Convert 4/8 and 5/16 into like fractions.
As 16 is twice 8, it is easy to make 16 the common denominator.
\(\frac{4}{8}=\frac{4 \times 2}{8 \times 2}=\frac{8}{16}\) Thus, 8/16 and 5/16 are the required like fractions.
Example (3) Find a common denominator for 4/7 and 3/4.
The number 28 is a multiple of both 7 and 4. So, make 28 the common denominator.
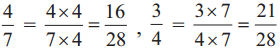. Therefore, 16/28 and 21/28 are the required like fractions.
Fractions Problem Set 17 Additional Important Questions and Answers
Question 1.
Find two equivalent fractions for each of the following fraction:
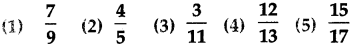
Solution:
